この問題のポイント
立体の切り口の辺は必ず立体の表面の上にある!
どの面とどの面が平行かも利用しながら切り口の図形を考えよう!
「この点とこの点を通る平面で切ったときの切り口の図形は?」など、切り口の図形を考えるときのコツは、問題で指定された点を立体の表面を通るように結ぶということです。立体を切ってできる図形なので、切り口の辺は必ず立体の表面の上にあるからです。
この説明だけではわかりにくいと思いますから、下の図を使って説明してみましょう。問題にあった立方体の点$E$,$G$ともう1点$X$を通る平面で切ったときの切り口を考えるとします。
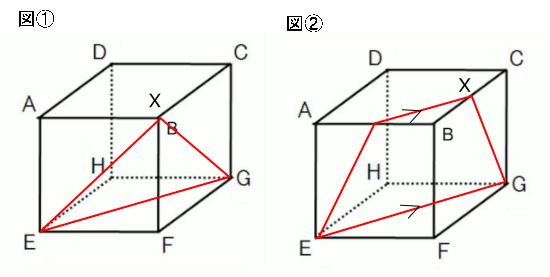
図①は点$X$が点$B$と重なっていた場合の切り口です。$EG$,$GX$,$XE$は面$HEFG$,$BFGC$,$AEFB$の上を通ります。よって、そのまま3点を結ぶことができるので、切り口の図形は三角形となります。
一方、図②は点$X$が辺$BC$上にある場合の切り口です。$EG$,$GX$はさっきと同じように立方体の表面上を通りますが、$XE$については表面上を通りません。
こういうときは、すでに直線をひいた面と平行な面に直線をひくことで点をつないでいくことを考えましょう。$EG$のある面$HEFG$と平行な面である$DABC$に$EG$と平行で$X$を通る直線をひきます。その直線の端の点と$E$を結ぶ直線は面$AEFB$の上にひけますから、このときの切り口の図形は台形となるわけです。
(1)この問題では、点$P$は$F$→$B$→$C$→$D$→$H$と動きます。よって、点$P$が辺$FB$,$BC$,$CD$,$DH$それぞれの上にあるときで切り口の図形はちがうはずです。さっき説明したやりかたで切り口の図形を考えるとこうなります。
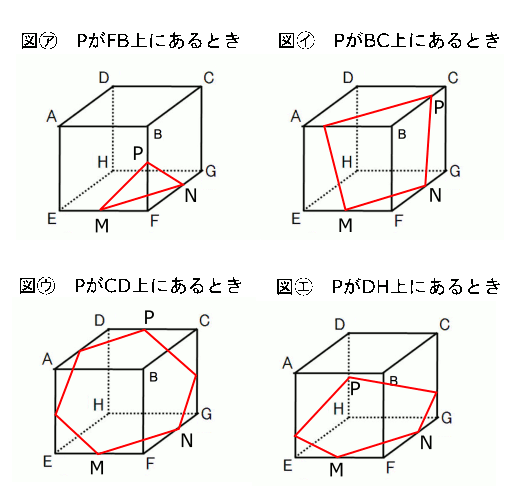
このように、4種類の図形が考えられます。三角形,四角形,五角形,六角形ということで、$n$にあてはまるのは3,4,5,6ということになります。
(2)切り口が三角形になるときは図㋐にあるとおり、点$P$が$FB$上にあるときです。そして、点$P$が$FB$の中点にあれば、$PM$,$MN$,$NP$は立方体の辺の中点どうしを結んだ線分ということで同じ長さになり、$△PMN$は正三角形になります。
立方体の1辺の長さは6cmですから、このときの$FP$の長さは3cmです。点$P$は毎秒1cmの速さで移動するので、$F$を出発してから3秒後に$FP$の長さは3cmとなり、切り口は正三角形になります。
(3)さっきの(2)と同じように考えます。切り口が六角形になるときは図㋒にあるとおり、点$P$が$CD$上にあるときです。そして、点$P$が$CD$の中点にあれば、切り口は正六角形になります。
ということは、このときの$CP$の長さは3cmですが、その前に点$P$は$FB$の6cmと$BC$の6cmをすでに通っています。つまり、点$P$は6+6+3 = 15cmの長さを通ったということになるので、$F$を出発してから15秒後ということになるわけです。
(4)点$P$が$F$を出発してから11秒後ということは、$FB$の6cmを通って$BC$上を5cm通ったタイミングということになります。つまり、点$P$は$BC$上にあるので、図㋑のとおり、切り口は四角形だといえます。
ちなみに、なぜ四角形になるかについてはわかりますか?$MN$や$NP$は立方体の面の上に直線をひけますが、$PM$は立方体の面の上に直線をひけません。そこで、$MN$のある面$HEFG$と平行な面である$DABC$に$MN$と平行な直線をひく必要がありますね?これにより、切り口の図形が四角形となるわけです。
ということは、この四角形は1組の辺が平行になっています。1組の辺が平行な四角形は台形です。このように、特別な形である図形については、特に入試問題ではそのことがわかる図形の名称で答えるべきです。なので、単なる「四角形」と答えるのではなく、「台形」と答えるべきでしょう。
答え.
(1)$n$ = 3,4,5,6
(2)3秒後
(3)15秒後
(4)台形(等脚台形)