この問題のポイント
P,Qが同じ側にあって∠APB=∠AQBが成り立つなら、4点A,B,P,Qは同じ円周上にある!
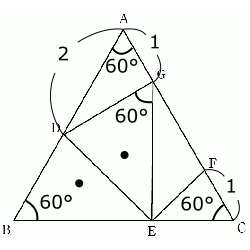
(1)考えやすくするために、まず問題文で与えられた角度や長さを図に書き込みます。また、そこからわかる角度や長さも書き込みましょう。たとえば、$△ABC$は正三角形なので三角形の1つの角度は60°です。そして、$△BDE$≡$△GDE$ですから、$∠DBE$に対応する角である$∠DGE$も60°です。
書き込んでいくと右の図のようになります。これを見ると、$△ADG$は、長さが1と2の辺があり、その間の角が60°となっています。これは過去の「特別な直角三角形の辺の比」の問題で書かれた解説にもありますが、辺の長さの比が$1$:$2$:\( \sqrt{3} \)の直角三角形の形ですね?
これより、$∠DGA$は90°とわかります。ということは、$∠CGE$の大きさは
180°-60°-90° = 30°
今度は$△GCE$に着目します。$∠CGE$は30°と求まり、$△ABC$は正三角形なので$∠GCE$は60°とわかっています。ということは、三角形の1つの外角はそれと隣り合わない2つの内角の和に等しいので、
$∠GEB$ = 30°+60° = 90°
$△BDE$≡$△GDE$なので、$∠DEB$と$∠DEG$の大きさは同じはずです。よって、$∠DEG$の大きさは
90°÷2 = 45°です。
この問題では、いきなり$∠DEG$の大きさを求めることは難しいでしょう。そのようなときは急がず、今のようにまず問題文で与えられた角度などの条件から、「そうするとここが求まる」「次にここもわかるな」と考えていきましょう。そのような順序で求まったものが、問題を解くときの重大なヒントを突然生み出していくことがあります。
(2)さっきの(1)の解説にあったとおり、$△ADG$は辺の長さの比が$1$:$2$:\( \sqrt{3} \)の直角三角形です。よって、$DG$の長さは\( \sqrt{3} \)です。
そして$△BDE$≡$△GDE$ですから、$DG$に対応する辺である$DB$の長さも\( \sqrt{3} \)です。
これより、$AD$ = 2でしたから、正三角形$ABC$の1辺の長さは\( 2+\sqrt{3} \)とわかります。
よって、\( AC = 2+\sqrt{3} \)なので、
\( FG = AC-AG-CF \)
\( = 2+\sqrt{3}-1-1 \)
\( = \sqrt{3} \)
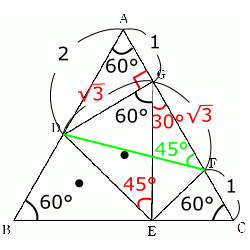
(3)ここまでの過程で求まった角度や長さの数値は書き込んでいくようにしましょう。右の図の赤色で書き込まれたものがその数値となります。さて、3点を通る円の半径を求めたい場合は、まず円の直径がどこになるかを探ってみましょう。直径に対する円周角は90°ですから、どこかに90°がないかを探すと大きなヒントになります。
$E$,$F$,$G$を通る円なので$EG$が直径になるのではないかと思われるのですが、そのまわりに90°となる角が見つかりませんし、計算などで考えても90°になる角がありません。ということは、$EG$ではなく別の辺が直径となる可能性が高いですね?
数値を書き込んだ図を見ると、$∠DGE$が60°,$∠CGE$が30°とわかるので、$∠DGF$は90°です。よって、図の緑色の線分$DF$が求める円の直径ではないかと考えることができます。ただし、これだけではまだ断定できません。$D$,$F$,$G$についてはOKなのですが、その円が$E$を通るかどうかがまだわからないためです。
$△DGF$を見てみると、$∠DEG$ = 90°,\( DG = \sqrt{3} \),そして(2)で求めたとおり\( FG = \sqrt{3} \)ですから、この三角形は直角二等辺三角形といえます。ということは、さっきの図の緑色で示されているとおり、$∠DFG$ = 45°です。
ここで、(1)で求めたとおり、$∠DEG$ = 45°でしたね?すると、この定理を使うことができます。
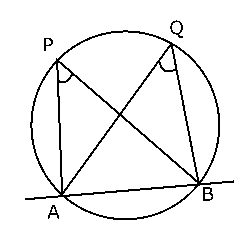
右の図のように、2点$P$,$Q$が直線$AB$について同じ側にあって、$∠APB$ = $∠AQB$ならば、4点$A$,$B$,$P$,$Q$は同じ円の円周上にある。
この問題では、$E$と$F$は$DG$について同じ側にあって、$∠DEG$ = $∠DFG$ = 45°ですから、$D$,$E$,$F$,$G$は同じ円の円周上にあります。よって、「3点$E$,$F$,$G$を通る円」とはこの円のことであり、その円の直径は$DF$ということになります。
$△DGF$は直角二等辺三角形なので、辺の長さの比は$1$:$1$:\( \sqrt{2} \)です(過去の「特別な直角三角形の辺の比」の問題で書かれた解説参照)。\( DG = \sqrt{3} \)なので、
\( DF = \sqrt{3}×\sqrt{2} = \sqrt{6} \)
なので、半径は\( \displaystyle \frac{\sqrt{6}}{2} \)です。
答え.
(1)45° (2)\( \sqrt{3} \) (3)\( \displaystyle \frac{\sqrt{6}}{2} \)