高校数学(3・C)の問題演習
令和3年12月12日
置換積分法
※千葉大学の入試問題です。(半角のみで入力し、分数は、たとえば3分の1なら[1]/[3]のように、[分子]/[分母]の形で入力すること)
\( \displaystyle I(a) = \int_0^π \frac{a\sin{θ}}{(a^2-2a\cos{θ}+1)^{\frac{3}{2}}}dθ \)(\( a>1 \))とする。
(1)$I(a)$を求めよ。
(2)\( \displaystyle \sum_{n=2}^\infty I(n) \)の値を求めよ。
令和3年8月29日
複素数平面と漸化式・極限
※学習院大学の入試問題です。
- すべて半角で入力すること。ただし、根号はルートの記号(√)を入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。虚数単位(i)の係数が分数の場合、たとえば係数が5分の3なら3i/5のように、分子のところに文字を含めること。
- 根号が入る場合は、たとえば「ルート2」なら√2のように√につづけて数字を入力すること。
- 実部と虚部があるものについては、実部を先に、虚部を後にした形で入力すること。
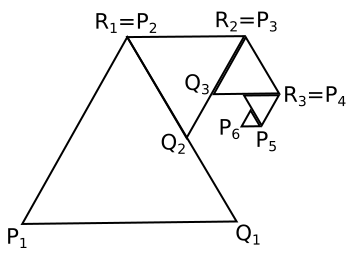
複素数平面上で正三角形$P_nQ_nR_n$($n$ = 1,2,3,…)を次の(A),(B)のように定める。
(A)
$P_1$,$Q_1$,$R_1$はそれぞれ複素数0,1,\( \displaystyle \frac{1}{2}+\frac{\sqrt{3}}{2}i \)で表される点である。
(B)
$P_{n+1} = R_n$
$Q_{n+1}$は$Q_nR_n$の中点
$R_{n+1}$は三角形$P_nQ_nR_n$の外部にある。
($n$ = 1,2,3,…)
(1)$R_2$,$R_3$を表す複素数$z_2$,$z_3$を求めよ。
(2)$R_n$を表す複素数$z_n$を求めよ。
(3)$α_n = z_{3n}$とおき、$α_n$の実部,虚部をそれぞれ$a_n$,$b_n$とする。\(\displaystyle \lim_{n \to \infty} a_n \),\(\displaystyle \lim_{n \to \infty} b_n \)を求めよ。
令和3年5月23日
複素数平面と図形
※名古屋工業大学の入試問題です。
- すべて半角で入力すること。ただし、±の記号だけは、「プラスマイナス」で変換して得られる記号を使うこと。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の3なら3a/5のように、分子のところに文字を含めること。
次の問いに答えよ。
(1)\( \displaystyle z+\frac{1}{z} = \sqrt{3} \)を満たす複素数$z$の値を求めよ。また、このとき\( \displaystyle α = z^{100}+\frac{1}{z^{100}} \)の値を求めよ。
(2)\( \displaystyle z+\frac{1}{z} \)が実数となるような複素数$z$が表す複素数平面上の点全体は、どのような図形を表すか。
(3)\( \displaystyle z+\frac{1}{z} \)が実数となる複素数$z$と、\( \displaystyle \left|w-\left(\frac{8}{3}+2i\right)\right| = \frac{2}{3} \)を満たす複素数$w$について、$|z-w|$の最小値を求めよ。
令和3年2月14日
逆関数の微分
※名古屋市立大学の入試問題です。
※入力は次の指示にしたがってください。
- すべて半角で入力すること。
- 分数は、たとえば3分の1なら[1]/[3]のように、[分子]/[分母]の形で入力すること。文字の係数が分数の場合、たとえばaの係数が5分の3なら[3a]/[5]のように、分子のところに文字を含めること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^を使って入力すること。
\( x≧0 \)で定義される関数\( f(x) = xe^{\frac{x}{2}} \)について、次の問いに答えよ。ただし、$e$は自然対数の底とする。
(1)$f(x)$の第1次導関数を$f'(x)$,第2次導関数を$f''(x)$とする。$f'(2)$,$f''(2)$を求めよ。
(2)$f(x)$の逆関数を$g(x)$,$g(x)$の第1次導関数を$g'(x)$,第2次導関数を$g''(x)$とする。$g'(2e)$,$g''(2e)$を求めよ。
令和2年11月1日
量と積分
※筑波大学の入試問題です。(基本的に半角で入力し、円周率についてはギリシア文字大文字のパイ($π$)で入力すること。分数をあらわすときは、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること)
曲線\( y = x(1-x) \)(\( \displaystyle 0≦x≦\frac{1}{2} \))を$y$軸の周りに回転してできる容器に、単位時間あたり一定の割合$V$で水を注ぐ。
(1)水面の上昇する速度$u$を水面の高さ$h$の関数として表せ。
(2)空の容器に水がいっぱいになるまでの時間を求めよ。
