この問題のポイント
複素数平面では|x-a| = |x-b|は二等分線、|x-a| = rは円をあらわす!
(1)二次方程式\( \displaystyle z+\frac{1}{z} = \sqrt{3} \)を解くと、\( z \neq 0 \)より、両辺に$z$をかけて、
\( z^2+1 = \sqrt{3}z \)
\( z^2-\sqrt{3}z+1 = 0 \)
\( \displaystyle z = \frac{-(-\sqrt{3})±\sqrt{(-\sqrt{3})^2-4・1・1}}{2・1} \)
\( \displaystyle ∴z = \frac{\sqrt{3}±i}{2} \)
次に、\( \displaystyle z^{100}+\frac{1}{z^{100}} \)の値について考えましょう。もちろん、100乗をふつうに計算していくのは無理があります。複素数では、ド・モアブルの定理、\( (\cos{θ}+i\sin{θ})^n = \cos{nθ}+i\sin{nθ} \)が利用できますから、これを利用することを考えましょう。
\( \displaystyle z = \frac{\sqrt{3}±i}{2} \)を極形式になおすと、\( \displaystyle z = \cos{\left(±\frac{π}{6}\right)}+i\sin{\left(±\frac{π}{6}\right)} \)
これで計算していくと、
\begin{eqnarray} &&z^{100}+\frac{1}{z^{100}}\\ &&= z^{100}+z^{-100}\\ &&= \left\{\cos{\left(±\frac{π}{6}\right)}+i\sin{\left(±\frac{π}{6}\right)}\right\}^{100}\\ &&~~~~+\left\{\cos{\left(±\frac{π}{6}\right)}+i\sin{\left(±\frac{π}{6}\right)}\right\}^{-100}\\ &&= \left\{\cos{\left(±\frac{100π}{6}\right)}+i\sin{\left(±\frac{100π}{6}\right)}\right\}\\ &&~~~~+\left\{\cos{\left(\mp\frac{100π}{6}\right)}+i\sin{\left(\mp\frac{100π}{6}\right)}\right\}\\ &&= \cos{\left(±\frac{50π}{3}\right)}+i\sin{\left(±\frac{50π}{3}\right)}\\ &&~~~~+\cos{\left(\mp\frac{50π}{3}\right)}+i\sin{\left(\mp\frac{50π}{3}\right)}\\ &&= \cos{\left(±\frac{2π}{3}\right)}+i\sin{\left(±\frac{2π}{3}\right)}\\ &&~~~~+\cos{\left(\mp\frac{2π}{3}\right)}+i\sin{\left(\mp\frac{2π}{3}\right)}\\ &&= -\frac{1}{2}±\frac{\sqrt{3}}{2}i-\frac{1}{2}\mp\frac{\sqrt{3}}{2}i\\ &&= -1\\ \end{eqnarray}
(2)複素数において、$z$が実数ならば\( z = \overline{z} \)が必要十分条件ということを利用して考えると、
\( \displaystyle z+\frac{1}{z} = \overline{z+\frac{1}{z}} \)
が必要十分条件ということになります。
これはつまり、\( \displaystyle z+\frac{1}{z} = \overline{z}+\frac{1}{\overline{z}} \)
そして、分母があると考えにくいのでこの式の両辺に\( z\overline{z} \)、つまり\( |z|^2 \)をかけると、
\begin{eqnarray} &&z|z|^2+\overline{z} = \overline{z}|z|^2+z\\ &&z|z|^2+\overline{z}-\overline{z}|z|^2-z = 0\\ &&|z|^2(z-\overline{z})-(z-\overline{z}) = 0\\ &&(|z|^2-1)(z-\overline{z}) = 0\\ \end{eqnarray}
よって、\( |z|^2-1 = 0 \)または\( z-\overline{z} = 0 \)が成立することになります。
\( |z|^2-1 = 0 \)とは、\( |z|^2 = 1 \)、つまり\( |z| = 1 \)
\( z-\overline{z} = 0 \)とは、\( z = \overline{z} \)
ここで、複素数平面における図形がどういう式であらわされるか確認しましょう。
\( |z-a| = |z-b| \)
…これは$A(a)$との距離と$B(b)$との距離が等しいことを示しているので、線分$AB$の垂直二等分線を示す
\( |z-a| = r \)
…これは$A(a)$との距離がつねにrという数値で一定ということを示しているので、中心が点$A$、半径$r$の円を示す
これより、\( |z| = 1 \)は\( |z-0| = 1 \)と考えれば、原点が中心、半径が1の円ということを示していることになります。
そして、\( z = \overline{z} \)は、さっき示した実数である必要十分条件の式と同じなので、$z$が実数であることになるので、複素数平面上では実軸部分をあらわすことになります。ただし、もともとの\( \displaystyle z+\frac{1}{z} \)という式より、\( z \neq 0 \)ということに注意しないといけないので、正確には原点を除いた実軸部分ということになります。
(3)\( \displaystyle \left|w-\left(\frac{8}{3}+2i\right)\right| = \frac{2}{3} \)は、(2)の解説の赤枠内にある内容を参考にすると、$w$は複素数平面上では点\( \displaystyle \left(\frac{8}{3}+2i\right) \)が中心で半径が\( \displaystyle \frac{2}{3} \)の円の上にあるということになります。
そして、\( \displaystyle z+\frac{1}{z} \)が実数となるという条件なので、$z$は(2)で求めた図形の上にあります。$|z-w|$とは、複素数平面上では$z$と$w$の距離ということになるので、複素数平面上で$z$と$w$の最短距離となる場合を考えてその最短距離を求めればよいということになります。
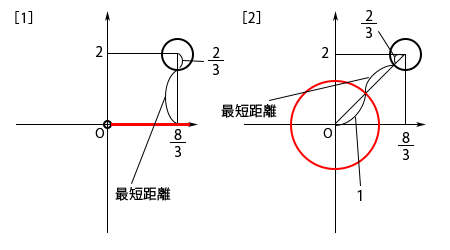
$z$と$w$の最短距離を考えると、上の図のようになります。[1]が$z$が原点を除いた実軸部分にある場合、[2]が$z$が原点が中心、半径が1の円上にある場合の図です。それぞれの図で、右上あたりにある小さな円が$w$、赤で示したものが$z$です。
[1]の場合において、$|z-w|$が最短となるのは、上の図の[1]に示したとおりですから、その長さは\( \displaystyle 2-\frac{2}{3} = \frac{4}{3} \)
[2]の場合において、$|z-w|$が最短となるのは、上の図の[2]に示したとおりです。2つの円の中心間の距離は\( \displaystyle \sqrt{\left(\frac{8}{3}\right)^2+2^2} = \sqrt{\frac{100}{9}} = \frac{10}{3} \)
そこから、2つの円の半径をいけばよいので、その長さは\( \displaystyle \frac{10}{3}-\left(1+\frac{2}{3}\right) = \frac{5}{3} \)
[1],[2]より、$|z-w|$の最小値は\( \displaystyle \frac{4}{3} \)です。
答え.
(1)\( \displaystyle z = \frac{\sqrt{3}±i}{2} \),$α$ = -1
(2)原点を除いた実軸部分と、原点が中心で半径が1の円
(3)\( \displaystyle \frac{4}{3} \)