この問題のポイント
体積、水面の高さ・面積はすべて時間の関数で表せる!
体積や水面の面積の変化率は、水面の高さの変化率を使った形に変形してみる!
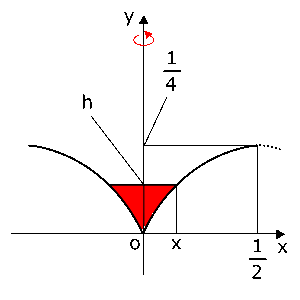
(1)容器にたまっていく水は、右の図における赤色の部分で示されます。ここで、右の図のように、$x$に対する水面の高さを$h$,体積を$v(h)$とすると、
\( \displaystyle v(h) = \int_0^h πx^2dy \)(ただし、\( \displaystyle 0≦h≦\frac{1}{4} \))
ここで、\( y = x(1-x) \)より、
\( y = x-x^2 \)
\( x^2-x+y = 0 \)
\( \displaystyle x = \frac{-(-1)±\sqrt{(-1)^2-4・1・y}}{2・1} \)
\( \displaystyle ∴x = \frac{1±\sqrt{1-4y}}{2} \)
図にあるとおり、\( \displaystyle 0≦x≦\frac{1}{2} \)より、\( \displaystyle x = \frac{1}{2}(1-\sqrt{1-4y}) \)なので、
\( \displaystyle x^2 = \frac{1}{4}(1-\sqrt{1-4y})^2 \)
\( \displaystyle = \frac{1}{4}(1-2\sqrt{1-4y}+1-4y) \)
\( \displaystyle = \frac{1}{4}(2-4y-2\sqrt{1-4y}) \)
\( \displaystyle = \frac{1}{2}(1-2y-\sqrt{1-4y}) \)
\( \displaystyle ∴v(h) = \frac{1}{2}π\int_0^h (1-2y-\sqrt{1-4y})dy \)
体積や、水面の高さ・面積はすべて時間がどれだけ経過したかによって決まりますから、このように、水の問題では時間の関数として数式にすると手がかりがつかめることが多いです。特に、この問題では、\( \displaystyle \frac{dv(h)}{dt} = V \),\( \displaystyle \frac{dh}{dt} = u \)なので、体積の変化率を、水面の高さの変化率を使った形になおしてみましょう。
$v(h)$を$t$で微分すると、
\( \displaystyle \frac{dv(h)}{dt} \)
\( \displaystyle = \frac{dv(h)}{dh}・\frac{dh}{dt} \)
\( \displaystyle = \frac{1}{2}π(1-2h-\sqrt{1-4h})・\frac{dh}{dt} \)
このようにできるので、
\( \displaystyle V = \frac{1}{2}π(1-2h-\sqrt{1-4h})・u \)
\( 2V = π(1-2h-\sqrt{1-4h})・u \)
よって、
\( \displaystyle \small{u = \frac{2V}{π}・\frac{1}{1-2h-\sqrt{1-4h}}} \)
\( \displaystyle \small{= \frac{2V}{π}・\frac{1-2h+\sqrt{1-4h}}{(1-2h-\sqrt{1-4h})(1-2h+\sqrt{1-4h})}} \)
\( \displaystyle \small{= \frac{2V}{π}・\frac{1-2h+\sqrt{1-4h}}{1-4h+4h^2-(1-4h)}} \)
\( \displaystyle \small{= \frac{2V}{π}・\frac{1-2h+\sqrt{1-4h}}{4h^2}} \)
\( \displaystyle \small{= \frac{V}{π}・\frac{1-2h+\sqrt{1-4h}}{2h^2}} \)
(2)水がいっぱいになるのは、\( \displaystyle h = \frac{1}{4} \)になったときです。
そこから考えると、容器の体積は、
\( \displaystyle \frac{1}{2}π\int_0^{\frac{1}{4}} (1-2y-\sqrt{1-4y})dy \)
\( \displaystyle = \frac{π}{2}\left[y-y^2+\frac{1}{6}\sqrt{(1-4y)^3}\right]_0^{\frac{1}{4}} \)
\( \displaystyle = \frac{π}{2}・\left(\frac{1}{4}-\frac{1}{16}-\frac{1}{6}\right) \)
\( \displaystyle = \frac{π}{2}・\frac{1}{48} \)
\( \displaystyle = \frac{π}{96} \)
単位時間あたり$V$の割合で水を注ぐので、水がいっぱいになるまでの時間は、
\( \displaystyle \frac{π}{96}÷V = \frac{π}{96V} \)
答え.
(1)\( \displaystyle \frac{V}{π}・\frac{1-2h+\sqrt{1-4h}}{2h^2} \)
(2)\( \displaystyle \frac{π}{96V} \)