高校数学(1・A)の問題演習
ユークリッドの互除法
※2016(平成28)年のセンター試験の問題を参考に作られています。(すべて半角で入力すること)
不定方程式
\( 92x+197y = 1 \)
をみたす整数$x$,$y$の組の中で、$x$の絶対値が最小のものは
$x$ = アイ,$y$ = ウエ
である。不定方程式
\( 92x+197y = 10 \)
をみたす整数$x$,$y$の組の中で、$x$の絶対値が最小のものは
$x$ = オカキ,$y$ = クケ
である。
データの相関
※2016(平成28)年のセンター試験の問題を参考に作られています。(すべて半角で入力すること)
世界4都市(東京、O市、N市、M市)の2013年の365日の各日の最高気温のデータについて考える。
(1)次の3つの散布図は、東京、O市、N市、M市の2013年の365日の各日の最高気温のデータをまとめたものである。それぞれ、O市、N市、M市の最高気温を縦軸にとり、東京の最高気温を横軸にとってある。
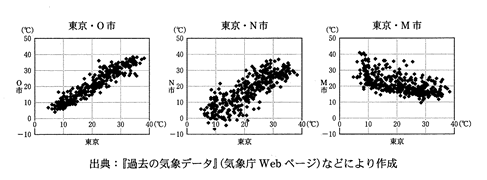
次のタ、チに当てはまるものを、下の[0]~④のうちから一つずつ選べ。ただし、解答の順序は問わない。
これらの散布図から読み取れることとして正しいものは、タとチである。
[0] 東京とN市、東京とM市の最高気温の間にはそれぞれ正の相関がある。
① 東京とN市の最高気温の間には正の相関、東京とM市の最高気温の間には負の相関がある。
② 東京とN市の最高気温の間には負の相関、東京とM市の最高気温の間には正の相関がある。
③ 東京とO市の最高気温の間の相関の方が、東京とN市の最高気温の間の相関より強い。
④ 東京とO市の最高気温の間の相関の方が、東京とN市の最高気温の間の相関より弱い。
(2)次のツ、テ、トに当てはまるものを、下の[0]~⑨のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
N市では温度の単位として摂氏(℃)のほかに華氏( ℉ )も使われている。華氏( ℉ )での温度は、摂氏(℃)での温度を\( \displaystyle \frac{9}{5} \)倍し、32を加えると得られる。例えば、摂氏10℃は、\( \displaystyle \frac{9}{5} \)倍し32を加えることで華氏50℉ となる。
したがって、N市の最高気温について、摂氏での分散を$X$、華氏での分散を$Y$とすると、\( \displaystyle \frac{Y}{X} \)はツになる。
東京(摂氏)とN市(摂氏)の共分散を$Z$、東京(摂氏)とN市(華氏)の共分散を$W$とすると、\( \displaystyle \frac{W}{Z} \)はテになる(ただし、共分散は2つの変量のそれぞれの偏差の積の平均値)。
東京(摂氏)とN市(摂氏)の相関係数を$U$、東京(摂氏)とN市(華氏)の相関係数を$V$とすると、\( \displaystyle \frac{V}{U} \)はトになる。
[0] \( \displaystyle -\frac{81}{25} \) ① \( \displaystyle -\frac{9}{5} \)
② -1 ③ \( \displaystyle -\frac{5}{9} \)
④ \( \displaystyle -\frac{25}{81} \) ⑤ \( \displaystyle \frac{25}{81} \)
⑥ \( \displaystyle \frac{5}{9} \) ⑦ 1
⑧ \( \displaystyle \frac{9}{5} \) ⑨ \( \displaystyle \frac{81}{25} \)
三角形の面積公式
※2017(平成29)年のセンター試験の問題です。(すべて半角で入力すること。区切れ目を・などで区切る必要はありません。)
$△ABC$において、\( AB = \sqrt{3}-1 \),\( BC = \sqrt{3}+1 \),$∠ABC$ = 60°とする。
(1)\( AC = \sqrt{\fbox{ア}} \)であるから、$△ABC$の外接円の半径は\( \sqrt{\fbox{イ}} \)であり
\( \displaystyle \sin∠BAC = \frac{\sqrt{\fbox{ウ}}+\sqrt{\fbox{エ}}}{\fbox{オ}} \)
である。ただし、ウ,エの解答の順序は問わない。
(2)辺$AC$上に点$D$を、$△ABD$の面積が\( \displaystyle \frac{\sqrt{2}}{6} \)になるようにとるとき
\( \displaystyle AB・AD = \frac{\fbox{カ}\sqrt{\fbox{キ}}-\fbox{ク}}{\fbox{ケ}} \)
であるから、\( \displaystyle AD = \frac{\fbox{コ}}{\fbox{サ}} \)である。
式の展開
※( )内の大学の入試問題を参考に作られています。(半角のみで入力すること)
(1)\( (a+b+c)^2+(a-b-c)^2-(-a+b-c)^2-(-a-b+c)^2 \)を展開したとき、$b^2$と$bc$の係数を求めよ。
(神戸国際大)
(1)\( \tiny{(a+b+c)^2+(a-b-c)^2-(-a+b-c)^2-(-a-b+c)^2} \)を展開したとき、$b^2$と$bc$の係数を求めよ。
(神戸国際大)
(2)\( A = x^3+x^2+x+1 \),\( B = x^3-x^2+x-1 \)とする。このとき、\( A^3-B^3 \)の展開式における$x^6$の係数を求めよ。
(防衛医科大学校)
円の内接・外接
※慶応義塾大学の入試問題です。(すべて半角数字のみ入力すること。たとえば答えが2けたなのに3けた分の空欄になっているなど、けた数が余分になっている場合、その余分な空欄の部分は0と入力すること。)
下図のように、3つの甲円が交わっている。上甲円に含まれる丙円と2つの乙円は上甲円に接している。2つの上乙円はそれぞれ2つの下甲円に接している。また、丙円は2つの下甲円に接している。さらに、下甲円は互いに接し、下乙円は2つの下甲円に接し、これら3つの円は一つの直線に接している。
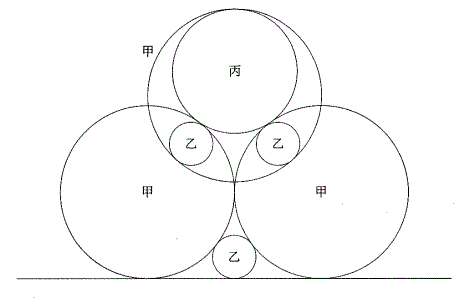
いま、乙円の直径を1寸とすると、甲円の直径は(1)(2)寸であり、
上甲円の中心は直線から\( \fbox{(3)}\fbox{(4)}+\sqrt{\fbox{(5)}\fbox{(6)}} \)寸離れた位置にある。
そして、丙円の直径は
\( \displaystyle \frac{\fbox{(7)}\fbox{(8)}+\fbox{(9)}\fbox{(10)}\sqrt{\fbox{(11)}\fbox{(12)}}}{\fbox{(13)}\fbox{(14)}} \)寸である。
