問題ページにもどる

この問題のポイント

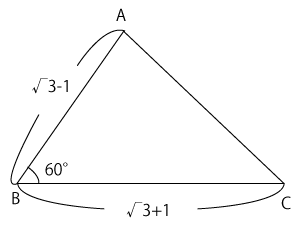
（１）問題文にあった$△ABC$を図示すると、右の図のようになります。この図より、この問題では、辺$a$，$c$の長さと$∠B$の大きさがわかっていることになります。

そして、$△ABC$について、2辺の長さとその間の角の大きさもわかっているということがこの図から読み取れます。このとき、残り1つの辺、$AC$の長さも余弦定理で求めることができます。2辺とその間の角がわかっていれば、余弦定理が使える問題は多いです。

$AC$を求めるということは、$b$を求めることですから、それについての余弦定理は、
\( b^2 = c^2+a^2-2ca\cos{B} \)

これを利用すると、

\begin{eqnarray} &&\small{b^2}\\ &&\small{= (\sqrt{3}-1)^2+(\sqrt{3}+1)^2-2(\sqrt{3}-1)(\sqrt{3}+1)\cos60°}\\ &&\small{= 3-2\sqrt{3}+1+3+2\sqrt{3}+1-2(3-1)\cos60°}\\ &&\small{= 8-2・2・\frac{1}{2}}\\ &&\small{= 6}\\ \end{eqnarray}

当然、$b$（= $AC$）は長さのことなので、\( AC = \sqrt{6} \)です。

外接円の半径のことも出題されていますが、外接円の半径は正弦定理で求めることができます。正弦定理では、三角形のうちの1つの角と、それに向かい合っている辺があれば利用することができます。この問題では、$∠B$だけがわかっていますから、
\( \displaystyle \frac{b}{\sin{B}} = 2R \)（$R$は外接円の半径）

この形の正弦定理を利用します。$b$（= $AC$）は\( \sqrt{6} \)なんですから、
\( \displaystyle \frac{\sqrt{6}}{\sin60°} = 2R \)
\( \displaystyle 2R = \sqrt{6}÷\frac{\sqrt{3}}{2} \)
\( \displaystyle R = \sqrt{6}・\frac{2}{\sqrt{3}}・\frac{1}{2} \)
よって、\( R = \sqrt{2} \)です。

そして、$∠BAC$とは$∠A$のことになりますが、これに向かい合う辺は$a$（= $BC$）です。なので、これについて正弦定理を使うと、
\( \displaystyle \frac{a}{\sin{A}} = 2R \)

\( R = \sqrt{2} \)なので、
\( \displaystyle \frac{\sqrt{3}+1}{\sin{A}} = 2\sqrt{2} \)
\( 2\sqrt{2}\sin{A} = \sqrt{3}+1 \)

\( ∴\sin{A} \)
\( \displaystyle = \frac{\sqrt{3}+1}{2\sqrt{2}} \)
\( \displaystyle = \frac{\sqrt{2}(\sqrt{3}+1)}{4} \)
\( \displaystyle = \frac{\sqrt{6}+\sqrt{2}}{4} \)

（２）$△ABD$の底辺と高さは示されていませんが、それでも面積を考えることができます。三角比を使えば、2辺とその間の角だけわかれば求めることができます。

S =	1	bcsinA =	1	casinB =	1	absinC
	2		2		2

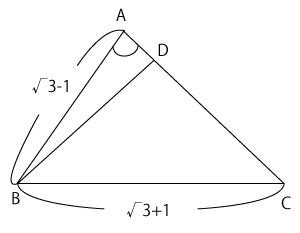
この公式を利用します。$△ABD$について、\( \sin{∠BAD} \)（右の図の印をつけた角）だけが\( \sin \)の値がわかっています。なぜなら、それは（１）で\( \sin{∠BAC} \)として求めたからです。公式にあてはめていくと、
\( \displaystyle \frac{\sqrt{2}}{6} = \frac{1}{2}AB・AD・\frac{\sqrt{6}+\sqrt{2}}{4} \)

左右両方に24をかけると、
\( 4\sqrt{2} = 3AB・AD・(\sqrt{6}+\sqrt{2}) \)

\( ∴AB・AD \)
\( \displaystyle = \frac{4\sqrt{2}}{3(\sqrt{6}+\sqrt{2})} \)
\( \displaystyle = \frac{4\sqrt{2}(\sqrt{6}-\sqrt{2})}{3(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \)
\( \displaystyle = \frac{4\sqrt{12}-4×2}{3×4} \)
\( \displaystyle = \frac{\sqrt{12}-2}{3} \)
\( \displaystyle = \frac{2\sqrt{3}-2}{3} \)

\( AB = \sqrt{3}-1 \)なので、
\( \displaystyle (\sqrt{3}-1)・AD = \frac{2\sqrt{3}-2}{3} \)

\( ∴AD \)
\( \displaystyle = \frac{2\sqrt{3}-2}{3(\sqrt{3}-1)} \)
\( \displaystyle = \frac{2(\sqrt{3}-1)}{3(\sqrt{3}-1)} \)
\( \displaystyle = \frac{2}{3} \)

答え．
ア　6　　　イ　2
ウエ　62（または26）　　　オ　4
カ　2　　　キ　3　　　ク　2　　　ケ　3
コ　2　　　サ　3