問題ページにもどる

この問題のポイント

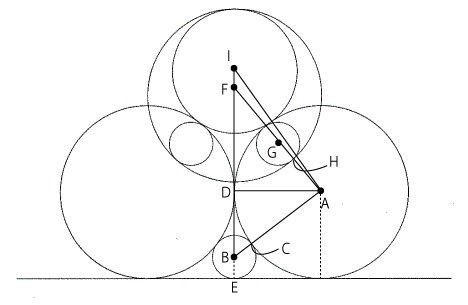
まず甲円の直径から考えます。この問題では、互いに接している円がいっぱいありますが、接している円どうしの距離などでは半径の和や差を計算するので、ここでは甲円の半径を利用して計算すると考えやすいかもしれませんので、その甲円の半径を$a$寸としましょう。

現時点では、乙円の直径しか数値がわかっていません。乙円と甲円が接しているところを探すと、たとえば下乙円と下甲円が接しているのがあります。その下甲円はもう一つの下甲円と接していますから、ここで接線をひくと上の図の$△ADB$は直角三角形になることがわかります。そうすると、三平方の定理を使えば長さを求めることができそうです。

ここで、甲円の半径を$a$寸とおいていたんですから、\( AD = a \)寸ですね。そして、$BC$については乙円の半径であって、直径が1寸なのですから、長さは1寸の半分です。よって、$AB$の長さは、\( \displaystyle AB = AC+BC = \left(a+\frac{1}{2}\right) \)寸

そして、$DB$についてですが、これも計算で求めることができます。$DE$は甲円の半径と長さが等しく、その長さから$BE$（乙円の半径）をひけばよいので、
\( \displaystyle DB = DE-BE = \left(a-\frac{1}{2}\right) \)寸

よって、$△ADB$において、三平方の定理より、
\( AB^2 = AD^2+DB^2 \)
\( \displaystyle \left(a+\frac{1}{2}\right)^2 = a^2+\left(a-\frac{1}{2}\right)^2 \)
\( \displaystyle a^2+a+\frac{1}{4} = a^2+a^2-a+\frac{1}{4} \)

整理すると、\( a^2-2a = 0 \)
\( a(a-2) = 0 \)
\( a = 0，2 \)
$a$というのは、甲円の半径のことなので、\( a = 2 \)寸ですね。

実際に解答するのは甲円の直径でしたから、答えは4寸となります。

次に、上甲円の中心と直線の距離を考えます。上の図でいうと$FE$の長さです（$F$は上甲円の中心です）。さっきと同じように、直角三角形をつくって解くやり方でできないか考えてみましょう。$DE$の長さはさっき甲円の半径と同じと考えていましたから、$FD$の長さがわかればよさそうです。そこで、$△AFD$で考えてみましょう。

$AD$の長さは甲円の半径と同じなので2寸です。
$AF$の長さですが、よく見ると、$FH$は甲円の半径で、$AH$の部分は甲円の半径から乙円の直径をひけば求まる長さだということがわかります。よって、\( AF = FH+AH = 2+(2-1) = 3 \)寸です。

注：ただし、この$AF$の長さは、上の図のとおり、上甲円と下甲円と上乙円の中心が一直線上にあるという前提で考えています。

これで$△AFD$において三平方の定理を使って$FD$を求めることができます。
\( AF^2 = AD^2+FD^2 \)
\( 3^2 = 2^2+FD^2 \)
\( FD^2 = 5 \)
\( FD＞0 \)より、\( FD = \sqrt{5} \)

よって、上甲円の中心と直線の距離は、
\( FE = DE+FD = (2+\sqrt{5}) \)寸です。

最後に考えるのは、丙円の直径です。さっき、甲円の半径を$a$として考えたのと同じように、ここでも丙円の半径を$b$として考えるとしましょう。上の図のように、丙円の中心を$I$とおきます。

さっきから直角三角形をつくって考えていましたが、ここでも同じように考えられるといいですよね？そこで、丙円がかかわる点を使って直角三角形をつくると$△IDA$ができます。これを利用できないかと考えるわけですね。

とりあえず、$AD$については2寸だとわかっています。そして、丙円と下甲円は接しているんですから、よく見ると$IA$の長さは丙円と下甲円の半径の和になっています。ですから、\( IA = (b+2) \)寸といえます。ということは、これで三平方の定理を使って$b$の方程式をたてることができれば、一気に丙円の半径を求めることができるはずですね。

そこで、$ID$の長さを考えることになるわけですが、さっき$FD$の長さが\( \sqrt{5} \)寸だと求まりましたので、あとは$IF$の長さだけわかればよさそうです。$I$は丙円の中心で、$F$は上甲円の中心ですね。よく見ると、丙円は上甲円に内接しているわけですから、$IF$はこの2つの円の半径の差と等しくなりますね。

ということは、\( IF = (2-b) \)寸ということになりますから、$ID$の長さは、
\( ID = IF+FD = (2-b+\sqrt{5}) \)寸

これで三平方の定理を使って方程式をたてると、
\( IA^2 = ID^2+AD^2 \)
\( (b+2)^2 = (2-b+\sqrt{5})^2+2^2 \)

このままだと計算がしにくいですから、$ID$に代入した値を\( 2+\sqrt{5}-b \)とすると、

\begin{eqnarray} &&\small{(b+2)^2 = (2+\sqrt{5}-b)^2+2^2}\\ &&\small{b^2+4b+4 = (2+\sqrt{5})^2-2b(2+\sqrt{5})+b^2+4}\\ &&\small{b^2+4b+4 = 4+4\sqrt{5}+5-4b-2\sqrt{5}b+b^2+4}\\ &&\small{(2\sqrt{5}+8)b = 4\sqrt{5}+9}\\ &&\small{b = \frac{4\sqrt{5}+9}{2\sqrt{5}+8}}\\ &&\small{b = \frac{(4\sqrt{5}+9)(2\sqrt{5}-8)}{(2\sqrt{5}+8)(2\sqrt{5}-8)}}\\ &&\small{b = \frac{40-32\sqrt{5}+18\sqrt{5}-72}{20-64}}\\ &&\small{b = \frac{-14\sqrt{5}-32}{-44}}\\ &&\small{b = \frac{7\sqrt{5}+16}{22}}\\ \end{eqnarray}

実際に解答するのは丙円の直径なので、これを2倍しないといけないので、\( \displaystyle \frac{16+7\sqrt{5}}{11} \)寸となります。

答え．
(1)　0　　　(2)　4
(3)　0　　　(4)　2　　　(5)　0　　　(6)　5
(7)　1　　　(8)　6　　　(9)　0　　　(10)　7　　　(11)　0　　　(12)　5
(13)　1　　　(14)　1