高校物理の問題演習
令和6年9月2日
キルヒホッフの法則
※東京理科大学の入試問題を参考に作られています。（すべて半角のみで入力すること）
次の文の の中に入れるべき正しい答えをそれぞれの解答群から選び、その番号を指定された欄に記入しなさい。必要なら同一番号を繰り返し用いてよい。
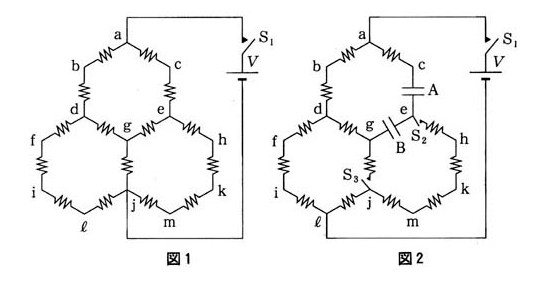
図1に示すように、抵抗$R$をもつ同じ導線15本と内部抵抗の無視できる起電力$V$の電池からなる回路がある。スイッチ$S_1$を閉じたとき、電池から流れ出る電流は (ア) \( \displaystyle ×\frac{V}{R} \)である。このとき、すべての接続点$a$～$m$のうちで、接続点$g$と同じ電位となる接続点は (イ)
次に、図2のようにスイッチ$S_1$を開き電池の負極側を接続点$j$から接続点$l$につなぎ換える。さらに導線$ce$と導線$eg$を取りのぞき、代わりに同じ電気容量$C$をもつコンデンサー$A$と$B$を接続する。はじめは、スイッチ$S_2$と$S_3$はともに閉じたままにしておき、スイッチ$S_1$を再び閉じる。十分時間がたった後での電池から流れ出る電流は、 (ウ) \( \displaystyle ×\frac{V}{R} \)である。また、コンデンサー$A$に蓄えられる電気量は、 (エ) \( ×CV \)であり、コンデンサー$B$に蓄えられる電気量は、 (オ) \( ×CV \)である。
この状態から引き続いて、スイッチ$S_2$を開きその後スイッチ$S_3$も開いた。このとき、コンデンサー$A$の接続点$e$側の極板にある電気量は、 (カ) (キ) \( ×CV \)であり、コンデンサー$B$の接続点$g$側の極板にある電気量は、 (ク) (ケ) \( ×CV \)となる。ただし、(カ)と(ク)には+または-の符号を記入しなさい。
(ア)，(ウ)，(エ)，(オ)，(キ)，(ケ)の解答群
00 \( \displaystyle \frac{2}{5} \) 01 \( \displaystyle \frac{3}{5} \) 02 \( \displaystyle \frac{1}{6} \) 03 \( \displaystyle \frac{5}{6} \)
04 \( \displaystyle \frac{1}{7} \)
05 \( \displaystyle \frac{2}{7} \) 06 \( \displaystyle \frac{6}{7} \) 07 \( \displaystyle \frac{1}{8} \)
08 \( \displaystyle \frac{3}{8} \) 09 \( \displaystyle \frac{7}{8} \)
10 \( \displaystyle \frac{2}{9} \) 11 \( \displaystyle \frac{5}{9} \)
12 \( \displaystyle \frac{7}{9} \) 13 \( \displaystyle \frac{3}{10} \) 14 \( \displaystyle \frac{7}{10} \)
15 \( \displaystyle \frac{9}{10} \)
16 \( \displaystyle \frac{2}{11} \) 17 \( \displaystyle \frac{3}{11} \) 18 \( \displaystyle \frac{7}{11} \) 19 \( \displaystyle \frac{9}{11} \)
20 \( \displaystyle \frac{3}{13} \) 21 \( \displaystyle \frac{7}{13} \) 22 \( \displaystyle \frac{11}{13} \) 23 \( \displaystyle \frac{3}{14} \)
24 \( \displaystyle \frac{9}{14} \)
25 \( \displaystyle \frac{11}{14} \) 26 \( \displaystyle \frac{7}{15} \) 27 \( \displaystyle \frac{11}{15} \)
(イ)の解答群
0 $d$と$e$である。 1 $f$と$h$である。
2 $i$と$j$と$k$である。
3 $l$と$m$である。
4 ない。