この問題のポイント
ややこしい回路で電流や電圧を考えるときは、まとめられる部品についてはまとめて簡略化し、キルヒホッフの法則を利用してみる!
問題の回路図を見てわかるとおり、かなり複雑な回路になっていますね。この問題のほかに、電源が複数の場所にあって電流がどう流れているかわかりにくいという問題が出題されることもあります。その問題を解くのに有効な手段として使えるのがキルヒホッフの法則です。
キルヒホッフの法則
- 第一法則…
回路の交点において、交点に入る電流の和と交点から出る電流の和は等しい
(つまり、交点に入ったからといって、電流の量は増えたり減ったりしない) - 第二法則…
閉回路(ひとまわりの閉じた回路)にて、経路上にある電源や抵抗の電位差をすべてたすと0となる
(つまり、抵抗で下がった電圧をすべて足した値と、起電力で上がった電圧をすべて足した値は等しい)
この法則を使ってどう考えるのかを、解説を通して見てみましょう!
(ア)
まず、問題で与えられた回路図のままだと考えにくいです。このような問題では、まとめられる部品はできるだけまとめて、回路をできるだけ簡略化していくのがコツです。
たとえば、$a$→$b$→$d$と$a$→$c$→$e$には抵抗が2本ありますが、それぞれ直列につながれていますから、合成抵抗で考えれば、$ad$間と$ae$間には$2R$の抵抗が1本あるのと同じと考えることができます。
同様に、$d$→$f$→$i$→$l$→$j$の経路と$e$→$h$→$k$→$m$→$j$の経路のそれぞれには4本の抵抗が直列につながれているので、この2本の経路には$4R$の抵抗が1本あるのと同じとみなせます。
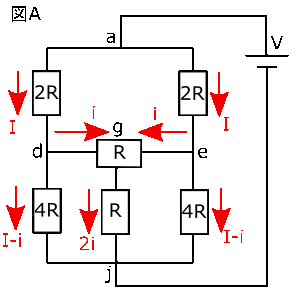
よって、図1の回路図は右の図のように簡略化させることができるわけです。そして、$a$から$j$までの経路は線対称になっていますから、回路を流れる電流を右の図のように$I$,$i$とおいて考えます。
この回路には$a$→$d$→$j$と$a$→$d$→$g$→$j$の2つの閉回路があることに気づきます($a$→$e$→$j$もありますが、$a$→$d$→$j$と線対称なので省略します)。この2つの閉回路について、キルヒホッフの第二法則を利用してみましょう。
$a$→$d$→$j$の閉回路については、
\( V = 2RI+4R(I-i) \)…①
$a$→$d$→$g$→$j$の閉回路については、
\( V = 2RI+Ri+R・2i \)…②
①を変形すると、\( 6RI-4Ri = V \)
②を変形すると、\( 2RI+3Ri = V \)
この2つを連立方程式にして解くと、\( \displaystyle I = \frac{7V}{26R} \),\( \displaystyle i = \frac{2V}{13R} \)
電流$I$は接続点$a$から枝わかれして流れたものなので、電池から流れた電流は$2I$ですから、
\( \displaystyle 2I = \frac{7V}{13R} = \frac{7}{13}×\frac{V}{R} \)
(イ)
点$j$の電位を基準として、$f$,$g$,$h$,$i$,$k$の電位を$V_f$,$V_g$,$V_h$,$V_i$,$V_k$とおいて考えると、
\( \displaystyle V_g = R・2i = R・2・\frac{2V}{13R} = \frac{4V}{13} \)
$j$から$f$,$h$それぞれまでの間には3本の抵抗があります。$f$,$h$の接続点を流れる電流は$I-i$とおけるので、
\( V_f = V_h \)
\( = 3R・(I-i) \)
\( \displaystyle = 3R・\left(\frac{7V}{26R}-\frac{2V}{13R}\right) \)
\( \displaystyle = 3R・\frac{3V}{26R} \)
\( \displaystyle = \frac{9V}{26}>V_g \)
$j$から$i$,$k$それぞれまでの間には2本の抵抗があります。$i$,$k$の接続点を流れる電流も$I-i$とおけるので、
\( V_i = V_k \)
\( = 2R・(I-i) \)
\( \displaystyle = 2R・\left(\frac{7V}{26R}-\frac{2V}{13R}\right) \)
\( \displaystyle = 2R・\frac{3V}{26R} \)
\( \displaystyle = \frac{3V}{13}<V_g \)
よって、同じ電位になる点はないということになります。
(ウ)
すべてのスイッチを閉じてしばらく時間がたった後なので、コンデンサーの充電は終わっていると考えることができます。そのため、$a$→$c$→$e$や$e$→$g$→$j$、$e$→$h$→$k$→$m$→$j$の経路には電流は流れないことになります。
つまり、$a$→$b$→$d$と電流が流れた後は、$d$→$f$→$i$→$l$という経路と$d$→$g$→$j$→$l$という経路の2つに分かれて、そして$l$で電流が再び合流するということになりますから、電源から流れる電流を$I'$とおくと、2つの経路それぞれに流れる電流は\( \displaystyle \frac{I'}{2} \)とおけます。
ここで、電源から$a$→$b$→$d$→$f$→$i$→$l$を通って電源に戻るという閉回路に着目すると、キルヒホッフの法則を利用することができます。$a$→$b$→$d$の間には抵抗が2本あるので合成抵抗は$2R$,$d$→$f$→$i$→$l$の間には抵抗が3本あるので合成抵抗は$3R$とおけますから、
\( \displaystyle V = 2RI'+3R・\frac{I'}{2} \)
これを$I'$について解くと、\( \displaystyle V = \frac{7R}{2}I' \)
\( \displaystyle I' = \frac{2V}{7R} = \frac{2}{7}×\frac{V}{R} \)
(エ)
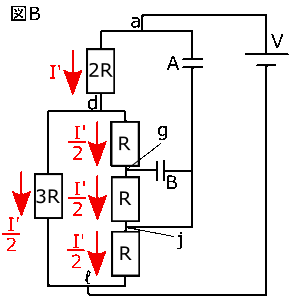
さっきの説明にもあったとおり、$a$→$c$→$e$や$e$→$g$→$j$、$e$→$h$→$k$→$m$→$j$の経路には電流は流れません。よって、図2の回路図は右の図Bのように簡略化させることができます。
そして、電源から流れる電流を$I'$とすると、$d$から$l$までの経路は2つありますから、それぞれの経路を流れる電流は\( \displaystyle \frac{I'}{2} \)とおけます。
図Bより、コンデンサー$A$にかかる電圧は$aj$間と等しいということになります。そこで、$l$を電位の基準にして考えると、$a$における電圧は$V$,$j$における電圧は\( \displaystyle R×\frac{I'}{2} \)とおけます。
すると、コンデンサー$A$に蓄えられる電気量は\( \displaystyle C×\left(V-R×\frac{I'}{2}\right) \)と求まります。さっき、\( \displaystyle I' = \frac{2V}{7R} \)と求めましたから、これも利用すると、
\( \displaystyle C×\left(V-R×\frac{V}{7R}\right) \)
\( \displaystyle = C×\left(V-\frac{V}{7}\right) \)
\( \displaystyle = \frac{6}{7}×CV \)
(オ)
図Bより、コンデンサー$B$にかかる電圧は$gj$間と等しいということになります。$gj$間の電圧は、その部分にある抵抗1本にかかる電圧と等しいことになるので\( \displaystyle R×\frac{I'}{2} \)とおけます。
コンデンサー$B$に蓄えられる電気量は
\( \displaystyle C×R×\frac{I'}{2} \)
\( \displaystyle = C×R×\frac{V}{7R} \)
\( \displaystyle = \frac{1}{7}×CV \)
(カ) ・ (キ)
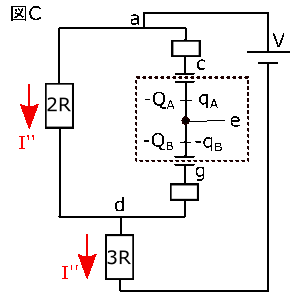
コンデンサー$A$の接続点$e$側の極板にある電気量を$q_A$,コンデンサー$B$の接続点$g$側の極板にある電気量を$q_B$とおきます。そして、コンデンサー$A$,$B$に蓄えられる電気量を$Q_A$,$Q_B$とおきます。
図2の回路図は右の図Cのように簡略化させることができますが、電荷保存の式は図のように、コンデンサー$A$,$B$それぞれの接続点$e$側の極板における帯電量は$-Q_A$,$-Q_B$とおけるので、次のようにおけます。
\( q_A-q_B = -Q_A-Q_B = -CV \)…③
そして、図Cの回路についてキルヒホッフの第二法則をあてはめると、
\( \displaystyle V = \frac{-q_A}{C}+\frac{-q_B}{C}+3RI'' \)…④
\( V = 2RI''+3RI'' \)…⑤
⑤より、\( V = 5RI'' \)なので、\( \displaystyle RI'' = \frac{1}{5}V \)
これを④に代入して、\( \displaystyle V = \frac{-q_A}{C}+\frac{-q_B}{C}+\frac{3}{5}V \)
\( \displaystyle \frac{-q_A}{C}+\frac{-q_B}{C} = \frac{2}{5}V \)
\( \displaystyle q_A+q_B = -\frac{2}{5}CV \)…⑥
③と⑥を連立方程式にして解くと、\( \displaystyle q_A = -\frac{7}{10}×CV \)が得られます。
(ク) ・ (ケ)
③と⑥を連立方程式にして解くと、\( \displaystyle q_B = \frac{3}{10}CV = +\frac{3}{10}CV \)が得られます。
答え.
(ア) …21
(イ) …4
(ウ) …05
(エ) …06
(オ) …04
(カ) …- (キ) …14
(ク) …+ (ケ) …13