高校数学(3・C)の問題演習
令和7年6月22日
同一平面上にある空間ベクトル
※( )内の大学の入試問題です。(すべて半角のみで入力し、分数は、たとえば分母が4で分子が1なら1/4のように、(分子)/(分母)の形で入力すること)
(1)空間内に、同一平面上にない4点$O$,$A$,$B$,$C$がある。$s$,$t$を\( 0<s<1 \),\( 0<t<1 \)をみたす実数とする。線分$OA$を1:1に内分する点を$A_0$,線分$OB$を1:2に内分する点を$B_0$,線分$AC$を\( s:(1-s) \)に内分する点を$P$,線分$BC$を\( t:(1-t) \)に内分する点を$Q$とする。さらに4点$A_0$,$B_0$,$P$,$Q$が同一平面上にあるとする。
(大阪大)
① $t$を$s$を用いて表せ。
② \( |\overrightarrow{OA}| \) = 1,\( |\overrightarrow{OB}| = |\overrightarrow{OC}| \) = 2,$∠AOB$ = 120°,$∠BOC$ = 90°,$∠COA$ = 60°,$∠POQ$ = 90°であるとき、$s$の値を求めよ。
(2)四角形$ABCD$を底辺とする四角錐$OABCD$は\( \overrightarrow{OA}+\overrightarrow{OC} = \overrightarrow{OB}+\overrightarrow{OD} \)を満たしており、0と異なる4つの実数$p$,$q$,$r$,$s$に対して4点$P$,$Q$,$R$,$S$を
\( \overrightarrow{OP} = p\overrightarrow{OA} \),\( \overrightarrow{OQ} = q\overrightarrow{OB} \),\( \overrightarrow{OR} = r\overrightarrow{OC} \),\( \overrightarrow{OS} = s\overrightarrow{OD} \)
によって定める。このとき$P$,$Q$,$R$,$S$が同一平面上にあれば
\( \displaystyle \frac{1}{p}+\frac{1}{r} = \frac{1}{q}+\frac{1}{s} \)が成立することを示せ。
(京都大)
令和6年12月22日
区分求積法
※( )内の大学の入試問題です。
※入力は次の指示にしたがってください。
- すべて半角で入力すること。ただし、根号はルートの記号(√)を入力すること。
- 根号が入る場合は、たとえば「ルート2」なら√2のように√につづけて数字を入力すること。
- 分数は、たとえば3分の1なら1/3のように、(分子)/(分母)の形で入力すること。
- 累乗は、たとえば「aの2乗」ならa^2のように、「○乗」の部分(指数)を^を使って入力すること。
- a,b,$π$など文字の係数が分数の場合、たとえばaの係数が5分の3なら3a/5、$π$の係数が2分のa+3(分母が2で分子がa+3)なら(a+3)$π$/2のように、分子のところに文字を含めること。
(1)次の極限値を求めよ。
(東京理科大)
① \( \displaystyle L_1 = \lim_{n \to \infty} \frac{(n+1)^a+(n+2)^a+…+(n+n)^a}{1^a+2^a+…+n^a} \)($a>0$)
② \( \displaystyle L_2 = \lim_{n \to \infty} \frac{1}{n^2}\sqrt[n] {{}_{4n} \mathrm{P}_{2n}} \)
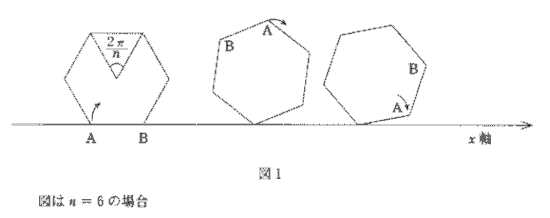
(2)半径1の円に内接する正$n$角形が$xy$平面上にある。ひとつの辺$AB$が$x$軸に含まれている状態から始めて、正$n$角形を図のように$x$軸上をすべらないようにころがし、再び点$A$が$x$軸に含まれる状態まで続ける。点$A$が描く軌跡の長さを$L(n)$とする。
(北海道大)
① $L(6)$を求めよ。
② \( \displaystyle \lim_{n \to \infty} L(n) \)を求めよ。