この問題のポイント
たくさんの足し算やシグマの極限を求めるときは区分求積法を利用するのが一つの方法!
シグマの外に1/n、シグマの中に●/nの形をつくるように式変形していく!
特に(1)の問題で明らかですが、たくさんの値が足し算になっている式やシグマであらわした式の極限を求める場合、区分求積法という方法が一つの解き方として使えます。
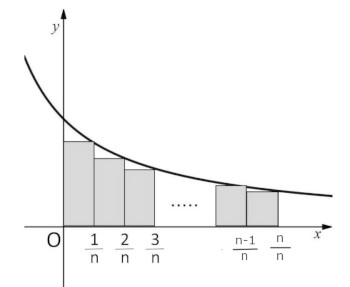
右の図のように、$y = f(x)$のグラフであるなめらかな曲線で囲まれた部分の面積を求めたいとなったときに、求めたい部分を$n$個の長方形に分けて考えます。この$n$の数が多くなれば多くなるほど、長方形は細かくなっていき、求めたい部分と合致するようになります。
このとき、それぞれの長方形の横の長さは、長方形は全部で$n$個あるんですから、\( \displaystyle \frac{1}{n} \)です。そして、それぞれの長方形の縦の長さは、$y = f(x)$上のグラフにおける$y$座標と同じはずですから、\( \displaystyle f\left(\frac{1}{n}\right) \),\( \displaystyle f\left(\frac{2}{n}\right) \),\( \displaystyle f\left(\frac{3}{n}\right) \),…となります。
ということは、長方形の面積全部を足すと、
\( \displaystyle \frac{1}{n}\left\{f\left(\frac{1}{n}\right)+f\left(\frac{2}{n}\right)+f\left(\frac{3}{n}\right)+…+f\left(\frac{n}{n}\right)\right\} \)
とあらわせます。
これをシグマを使ってあらわすと、
\( \displaystyle \frac{1}{n}\sum_{k=1}^n f\left(\frac{k}{n}\right) \)
とおけます。この$n$が大きくなればなるほど、つまり\( \infty \)に近づけていけばいくほど、長方形の数が増えて面積がより正確になっていきますね。
そして、面積を求めるのは積分でもできました。積分する範囲は0から\( \displaystyle \frac{n}{n} \) = 1までですから、面積を積分の式であらわすと、\( \displaystyle \int_0^1 f(x)dx \)とおけます。
つまり、区分求積法とは、
\( \displaystyle \lim_{n \to \infty} \frac{1}{n}\sum_{k=1}^n f\left(\frac{k}{n}\right) = \int_0^1 f(x)dx \)
と置き換えることをいいます。\( \displaystyle \frac{1}{n} \)や\( \displaystyle \frac{k}{n} \)の形ができるように式を変形すれば、この方法が使えるので、どのように式を変形するかを見てみましょう。
(1)① 分子は$(n+k)^a$,分母は$k^a$という形になっているものがたくさん足し算されています。$(n+k)^a$と$k^a$について、それぞれを$n^{1+a}$で割ると、分子は
\( \displaystyle \frac{1}{n^{1+a}}(n+k)^a \)
\( \displaystyle = \frac{1}{n}・\frac{(n+k)^a}{n^a} \)
\( \displaystyle = \frac{1}{n}\left(\frac{n+k}{n}\right)^a \)
\( \displaystyle = \frac{1}{n}\left(1+\frac{k}{n}\right)^a \)
分母は
\( \displaystyle \frac{1}{n^{1+a}}k^a \)
\( \displaystyle = \frac{1}{n}・\frac{k^a}{n^a} \)
\( \displaystyle = \frac{1}{n}・\left(\frac{k}{n}\right)^a \)
とおけます。
よって、$L_1$は、このように変形できます。
\( \displaystyle \lim_{n \to \infty} \frac{\frac{1}{n}\left\{\left(1+\frac{1}{n}\right)^a+\left(1+\frac{2}{n}\right)^a+…+\left(1+\frac{n}{n}\right)^a\right\}}{\frac{1}{n}\left\{\left(\frac{1}{n}\right)^a+\left(\frac{2}{n}\right)^a+…+\left(\frac{n}{n}\right)^a\right\}} \)
\( \displaystyle = \lim_{n \to \infty} \frac{\displaystyle\frac{1}{n}\sum_{k=1}^n \left(1+\frac{k}{n}\right)^a}{\displaystyle\frac{1}{n}\sum_{k=1}^n \left(\frac{k}{n}\right)^a} \)
このように、\( \displaystyle \frac{k}{n} \)の形ができあがり、シグマの外側に\( \displaystyle \frac{1}{n} \)をつくることができたので、区分求積法を使うことができます。そのときは、シグマの外側の\( \displaystyle \frac{1}{n} \)を消し、\( \displaystyle \frac{k}{n} \)を$x$に置き換えて積分します。$a>0$なので、区分求積法により、分子・分母ともに収束しますから、$L_1$は、
\( \displaystyle \frac{\displaystyle\int_0^1 (1+x)^adx}{\displaystyle\int_0^1 x^a} \)とおけます。
分子については、
\( \displaystyle \int_0^1 (1+x)^adx \)
\( \displaystyle = \left[\frac{1}{a+1}(1+x)^{a+1}\right]_0^1 \)
\( \displaystyle = \frac{1}{a+1}(1+1)^{a+1}-\frac{1}{a+1}(1+0)^{a+1} \)
\( \displaystyle = \frac{1}{a+1}(2^{a+1}-1^{a+1}) \)
\( \displaystyle = \frac{1}{a+1}(2^{a+1}-1) \)
分母については、
\( \displaystyle \int_0^1 x^adx \)
\( \displaystyle = \left[\frac{1}{a+1}x^{a+1}\right]_0^1 \)
\( \displaystyle = \frac{1}{a+1}・1^{a+1}-\frac{1}{a+1}・0^{a+1} \)
\( \displaystyle = \frac{1}{a+1}・1 \)
\( \displaystyle = \frac{1}{a+1} \)
よって、
\( \displaystyle \frac{\displaystyle\int_0^1 (1+x)^adx}{\displaystyle\int_0^1 x^a} \)
\( \displaystyle = \frac{\frac{1}{a+1}(2^{a+1}-1)}{\frac{1}{a+1}} \)
\( = 2^{a+1}-1 \)
② \( \displaystyle A_n = \frac{1}{n^2}\sqrt[n] {{}_{4n} \mathrm{P}_{2n}} \)とおくと、
\( \displaystyle A_n = \sqrt[n] {\left(\frac{1}{n^2}\right)^n\left\{4n(4n-1)(4n-2)…(2n+1)\right\}} \)
\( \displaystyle = \sqrt[n] {\frac{1}{n^{2n}}\left\{4n(4n-1)(4n-2)…(2n+1)\right\}} \)
\( \displaystyle = \sqrt[n] {\frac{4n}{n}・\frac{4n-1}{n}・\frac{4n-2}{n}…・\frac{2n+1}{n}} \)
\( \displaystyle = \sqrt[n] {\frac{2n+2n}{n}・\frac{2n+2n-1}{n}・\frac{2n+2n-2}{n}…・\frac{2n+1}{n}} \)
\( \displaystyle \small{= \left(\frac{2n+2n}{n}・\frac{2n+2n-1}{n}・\frac{2n+2n-2}{n}・…・\frac{2n+1}{n}\right)^{\frac{1}{n}}} \)
区分求積法ではシグマが関係しているので、かけ算の形になっているこの式を足し算の形に変換するために、対数をとります。
\( \log A_n \)
\( \displaystyle \small{= \frac{1}{n}\log \left(\frac{2n+2n}{n}・\frac{2n+2n-1}{n}・\frac{2n+2n-2}{n}…・\frac{2n+1}{n}\right)} \)
\( \displaystyle \small{= \frac{1}{n}\log \left\{\left(2+\frac{2n}{n}\right)\left(2+\frac{2n-1}{n}\right)…\left(2+\frac{1}{n}\right)\right\}} \)
\( \displaystyle \small{= \frac{1}{n}\left\{\log \left(2+\frac{2n}{n}\right)+\log \left(2+\frac{2n-1}{n}\right)+…+\log \left(2+\frac{1}{n}\right)\right\}} \)
\( \displaystyle \small{= \frac{1}{n}\sum_{k=1}^{2n} \log \left(2+\frac{k}{n}\right)} \)
これの極限を考えれば、区分求積法により積分の形に変換できますが、注意点が1つあります。シグマをするのは$k$が1から$2n$までなんですから、このページの上にて説明した考えを使うと、長方形が$2n$個あることになります。つまり、長方形の個数が2倍になるわけなので、積分する区間も2倍になるので、0から2までの範囲で積分します。
\( \displaystyle \lim_{n \to \infty} \log A_n \)
\( \displaystyle = \lim_{n \to \infty} \frac{1}{n}\sum_{k=1}^{2n} \log \left(2+\frac{k}{n}\right) \)
\( \displaystyle = \int_0^2 \log (2+x)dx \)
\( \displaystyle = \left[(2+x)\log (2+x)\right]_0^2-\int_0^2 (2+x)\frac{1}{2+x}dx \)
\( \displaystyle = \left[(2+x)\log (2+x)\right]_0^2-\left[x\right]_0^2 \)
\( = 4\log 4-2\log 2-2 \)
\( \displaystyle = \log \frac{64}{e^2} \)
よって、
\( \displaystyle L_2 = \lim_{n \to \infty} A_n = \frac{64}{e^2} \)
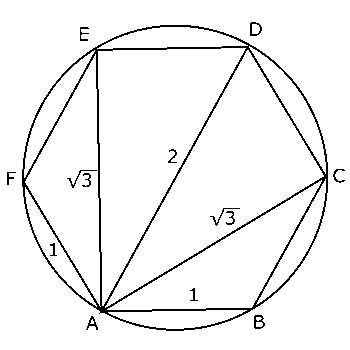
(2)① 正6角形を考えることになります。それぞれの角の角度は\( \displaystyle \frac{π}{3} \),半径1の円に内接するので、右の図において$AB = 1$です。はじめに点$A$は点$B$を中心に半径1の円周上を中心角\( \displaystyle \frac{π}{3} \)だけ回転することになります。
次に、点$C$が回転の中心になりますから、点$A$は点$C$を中心に半径が\( AC = \sqrt{3} \)の円周上を中心角\( \displaystyle \frac{π}{3} \)だけ回転します。その次は、点$D$,点$E$,点$F$と中心角\( \displaystyle \frac{π}{3} \)の回転を続けます。
よって、
$L(6)$
\( \displaystyle = \frac{π}{3}(1+\sqrt{3}+2+\sqrt{3}+1) \)
\( \displaystyle = \frac{4+2\sqrt{3}}{3}π \)
② さっきの①で考えたときと同様に、正$n$角形の頂点を$A$,$B_1$,$B_2$,…,$B_{n-1}$とすると、
\( \displaystyle L(n) = \frac{2π}{n}×\sum_{k=1}^{n-1} AB_{k-1} \)とおけます。
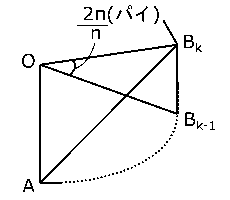
ここで、右の図でも示されているとおり、\( \displaystyle ∠AOB_k = k×\frac{2π}{n} \)であり、半径1の円に内接しているんですから、余弦定理を使って、
\( \displaystyle AB_k^2 = 1^2+1^2-2・1・1・\cos{\frac{2kπ}{n}} \)
\( \displaystyle = 2\left(1-\cos{\frac{2kπ}{n}}\right) \)
\( \displaystyle = 4\sin^2{\frac{kπ}{n}} \)
これより、\( \displaystyle AB_k = 2\sin{\frac{kπ}{n}} \)
よって、
\( \displaystyle L(n) = \frac{2π}{n}×\sum_{k=1}^{n-1} 2\sin{\frac{kπ}{n}} \)
\( \displaystyle = 4×\frac{π}{n}×\sum_{k=1}^{n-1} \sin{\frac{kπ}{n}} \)
\( \sin0 = 0 \)なので、\( \displaystyle 4×\frac{π}{n}×\sum_{k=0}^{n-1} \sin{\frac{kπ}{n}} \)としてしまいます。
こうすることで、\( \displaystyle \frac{π}{n} = π×\frac{1}{n} \),\( \displaystyle \frac{kπ}{n} = π×\frac{k}{n} \)と置き換えれば区分求積法を利用することができるからです。すなわち、
\( \displaystyle \lim_{n \to \infty} L(n) \)
\( \displaystyle = 4×\int_0^π \sin{x}dx \)
\( = 4×\left[\cos{x}\right]_0^π \)
\( = 4(-\cosπ+\cos0) \)
= 4(1+1) = 8
答え.
(1)
① \( L_1 = 2^{a+1}-1 \)
② \( \displaystyle L_2 = \frac{64}{e^2} \)
(2)
① \( \displaystyle L(6) = \frac{4+2\sqrt{3}}{3}π \)
② \( \displaystyle \lim_{n \to \infty} L(n) \) = 8