この問題のポイント
長方形の辺の方程式は「D = 0」と「傾きどうしの積が-1」を利用して求める!
面積は辺と原点との距離を利用して求める!
(1)求める直線の方程式を\( y = mx+n \)とおきます。$n$が求まればこの問題が解けたことになります。
\( y = mx+n \)を$C$の方程式の\( \displaystyle \frac{x^2}{16}+\frac{y^2}{9} = 1 \)に代入して、
\( \displaystyle \frac{x^2}{16}+\frac{(mx+n)^2}{9} = 1 \)
\( 9x^2+16(mx+n)^2 = 144 \)
\( 9x^2+16m^2x^2+32mnx+16n^2-144 = 0 \)
\( (16m^2+9)x^2+32mnx+16n^2-144 = 0 \)
直線と$C$は接していますから、この方程式は重解をもちます。ということは、この方程式の判別式は0と等しいです。
この方程式の判別式は、
\( \displaystyle \frac{D}{4} = (16mn)^2-(16m^2+9)(16n^2-144) \)
よって、
\( (16mn)^2-(16m^2+9)(16n^2-144) = 0 \)
\( 16m^2n^2-(16m^2+9)(n^2-9) = 0 \)
\( 16m^2n^2-16m^2n^2+144m^2-9n^2+81 = 0 \)
\( 9n^2 = 144m^2+81 \)
\( n^2 = 16m^2+9 \)
\( n = ±\sqrt{16m^2+9} \)
これより、求める直線の方程式は
\( y = mx+\sqrt{16m^2+9} \),\( y = mx-\sqrt{16m^2+9} \)
の2本です。
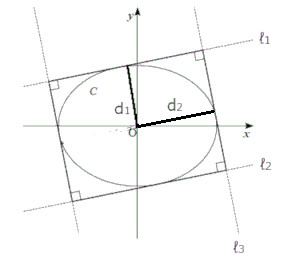
(2)\( m \neq 0 \)のとき、$C$と長方形の関係は右の図のようになります。さっきの(1)で求めた方程式の直線は$l_1$,$l_2$ということになります。この長方形の面積を求めるには縦の長さと横の長さを考える必要があります。
縦の長さについてですが、$l_1$と楕円の中心である原点との距離を右の図のように$d_1$とすると、
$l_1$の方程式は\( y = mx+\sqrt{16m^2+9} \),つまり\( mx-y+\sqrt{16m^2+9} = 0 \)なので、
\( \displaystyle d_1 = \frac{|m・0-0+\sqrt{16m^2+9}|}{\sqrt{m^2+(-1)^2}} \)
\( \displaystyle = \frac{\sqrt{16m^2+9}}{\sqrt{m^2+1}} \)
長方形の縦の長さは$2d_1$と等しいので、縦の長さは\( \displaystyle \frac{2\sqrt{16m^2+9}}{\sqrt{m^2+1}} \)とおけます。
次に、$l_1$と垂直に交わる直線についてですが、垂直に交わっているということは、この2本の傾きの積は-1なので、$l_1$の方程式の$m$を\( \displaystyle -\frac{1}{m} \)に置き換えることにより求められますから、$l_3$の方程式は、
\( \displaystyle y = -\frac{1}{m}x+\sqrt{\frac{16}{m^2}+9} \)
よって、$l_3$と原点との距離を$d_2$とすると、$l_3$の方程式は\( \displaystyle -\frac{1}{m}x-y+\sqrt{\frac{16}{m^2}+9} = 0 \)となるので、
\( \displaystyle d_2 = \frac{|-\frac{1}{m}・0-0+\sqrt{\frac{16}{m^2}+9}|}{\sqrt{\left(-\frac{1}{m}\right)^2+(-1)^2}} \)
\( \displaystyle = \frac{\sqrt{\frac{16+9m^2}{m^2}}}{\sqrt{\frac{1+m^2}{m^2}}} \)
\( \displaystyle = \frac{\frac{\sqrt{9m^2+16}}{m}}{\frac{\sqrt{m^2+1}}{m}} \)
\( \displaystyle = \frac{\sqrt{9m^2+16}}{\sqrt{m^2+1}} \)
長方形の横の長さは$2d_2$と等しいので、横の長さは\( \displaystyle \frac{2\sqrt{9m^2+16}}{\sqrt{m^2+1}} \)とおけます。
よって、
\( S(m) = 2d_1・2d_2 \)
\( \displaystyle = \frac{2\sqrt{16m^2+9}}{\sqrt{m^2+1}}・\frac{2\sqrt{9m^2+16}}{\sqrt{m^2+1}} \)
\( \displaystyle = \frac{4\sqrt{16m^2+9}\sqrt{9m^2+16}}{m^2+1} \)
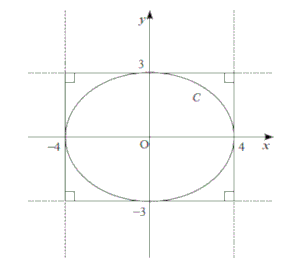
また、\( m = 0 \)のとき、$C$と長方形の関係は右の図のようになるため、長方形の縦の長さは6,横の長さは8となるため、面積は48になります。
\( \displaystyle S(m) = \frac{4\sqrt{16m^2+9}\sqrt{9m^2+16}}{m^2+1} \)に\( m = 0 \)を代入すると、
\( \displaystyle S(0) = \frac{4\sqrt{16・0^2+9}\sqrt{9・0^2+16}}{0^2+1} \)
\( = 4\sqrt{9}\sqrt{16} \)
= 4・3・4 = 48
よって、\( m = 0 \)のときも成立するので、\( \displaystyle S(m) = \frac{4\sqrt{16m^2+9}\sqrt{9m^2+16}}{m^2+1} \)です。
(3)最大値を求めるために(2)で求めた$S(m)$を変形します。
\( \displaystyle S(m) = \frac{4\sqrt{16m^2+9}\sqrt{9m^2+16}}{m^2+1} \)
\( \displaystyle = 4\sqrt{\frac{16m^2+9}{m^2+1}・\frac{9m^2+16}{m^2+1}} \)
\( \displaystyle = 4\sqrt{\frac{16m^2+16-7}{m^2+1}・\frac{9m^2+9+7}{m^2+1}} \)
\( \displaystyle = 4\sqrt{\left(16-\frac{7}{m^2+1}\right)・\left(9+\frac{7}{m^2+1}\right)} \)
ここで、\( \displaystyle t = \frac{7}{m^2+1} \)とおくと、2次関数\( f(t) = (16-t)(9+t) \)について、
\( f(t) = (16-t)(9+t) \)
\( = -t^2+7t+144 \)
\( = -(t^2-7t)+144 \)
\( \displaystyle = -\left(t^2-7t+\frac{49}{4}-\frac{49}{4}\right)+144 \)
\( \displaystyle = -\left(t^2-7t+\frac{49}{4}\right)+\frac{49}{4}+144 \)
\( \displaystyle = -\left(t-\frac{7}{2}\right)^2+\frac{625}{4} \)
となるので、$f(t)$は\( \displaystyle t = \frac{7}{2} \)のとき、最大値\( \displaystyle \frac{625}{4} \)をとります。\( \displaystyle t = \frac{7}{2} \)となるときの$m$の値は
\( \displaystyle \frac{7}{m^2+1} = \frac{7}{2} \)が成立するとき、つまり
\( m^2+1 = 2 \)
\( m = ±1 \)のときです。
このときの$S(m)$の値は、
\( \displaystyle 4\sqrt{\frac{625}{4}} \)
\( \displaystyle = 4・\frac{25}{2} \)
= 50です。
答え.
(1)\( y = mx+\sqrt{16m^2+9} \),\( y = mx-\sqrt{16m^2+9} \)
(2)\( \displaystyle S(m) = \frac{4\sqrt{16m^2+9}\sqrt{9m^2+16}}{m^2+1} \)
(3)50