この問題のポイント
OAのベクトル(OA→)とOBのベクトル(OB→)2本でsOA→+tOB→で表される点は、s≧0,t≧0,s+t≦1ならば△OABの周と内部に存在できる!
(1)余弦定理より、
\( \displaystyle \cos{∠AOB} = \frac{5^2+6^2-7^2}{2・5・6} \)
\( \displaystyle = \frac{12}{60} = \frac{1}{5} \)
$∠AOB$は$△OAB$の1つの角のため、180°より必ず小さいですから、\( \sin{∠AOB}>0 \)です。
\( ∴\sin{∠AOB} = \sqrt{1-\cos^2{∠AOB}} \)
\( \displaystyle = \sqrt{1-\left(\frac{1}{5}\right)^2} \)
\( \displaystyle = \sqrt{\frac{24}{25}} = \frac{2\sqrt{6}}{5} \)
三角形の面積は、2辺の長さとその間の角の\( \sin \)の値で求まるので、求める面積は、
\( \displaystyle \frac{1}{2}・5・6・\frac{2\sqrt{6}}{5} = 6\sqrt{6} \)
(2)\( \overrightarrow{OP} = s\overrightarrow{OA}+t\overrightarrow{OB} \)という式は、\( \overrightarrow{OA} \)と\( \overrightarrow{OB} \)の2本を使って点$P$がどの位置にあるかを示した式、つまり位置ベクトルを示した式です。\( s\overrightarrow{OA}+t\overrightarrow{OB} \)という式で与えられた位置ベクトルについて、次のようなことがいえます。
\( \overrightarrow{OA} \)と\( \overrightarrow{OB} \)の2本が0ベクトルでもなく、お互いに平行でないならば、\( \overrightarrow{OP} = s\overrightarrow{OA}+t\overrightarrow{OB} \)のとき、点$P$が存在できる範囲は
$s+t = 1$ならば直線$AB$
$s+t = 1$,$s≧0$,$t≧0$ならば線分$AB$
$s+t≦1$,$s≧0$,$t≧0$ならば$△OAB$の周とその内部
これを利用して、$s≧0$,$t≧0$,$s+t≦2$のときの点$P$が存在できる範囲を考えてみましょう。
$s = 2m$,$t = 2n$とすると、
\( \overrightarrow{OP} = 2m\overrightarrow{OA}+2n\overrightarrow{OB} \)
\( \overrightarrow{OP} = m・2\overrightarrow{OA}+n・2\overrightarrow{OB} \)
ここで、\( 2\overrightarrow{OA} = \overrightarrow{OC} \),\( 2\overrightarrow{OB} = \overrightarrow{OD} \)とすると、
$2m≧0$,$2n≧0$,$2m+2n≦2$、つまり$m≧0$,$n≧0$,$m+n≦1$であり、
\( \overrightarrow{OP} = m\overrightarrow{OC}+n\overrightarrow{OD} \)となります。
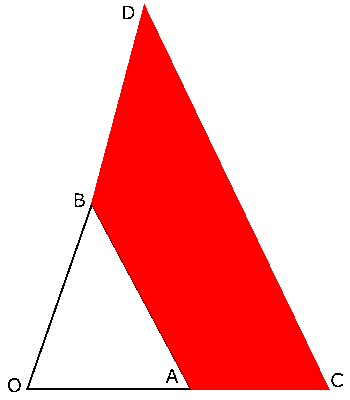
これより、点$P$の存在する範囲は右の図でいう$△OCD$の周と内部ということになります。これが$s+t≦2$のときの範囲ということですから、$1≦s+t≦2$のときの点$P$の存在する範囲は四角形$ACDB$(右の図の赤く塗られている部分)ということになります。
\( OC:OA = 2:1 \)ですから、$△OCD$と$△OAB$の相似比は2:1です。よって、$△OCD$と$△OAB$の面積比は\( 2^2:1^2 = 4:1 \)ですから、四角形$ACDB$の面積は、
\( △OCD-△OAB \)
\( = 4△OAB-△OAB \)
\( = 3△OAB \)
\( = 3・6\sqrt{6} = 18\sqrt{6} \)
この問題のように、$s$や$t$の範囲が与えられて位置ベクトルの範囲を考えることとなる問題では、$●●≦1$の形に変形して考えていくことがポイントになります。
(3)まず$s≧0$,$t≧0$,$1≦2s+t≦2$のときに点$P$が存在する範囲を考えます。$p = 2s$とおくと、\( \displaystyle s = \frac{1}{2}p \)なので、
\( \displaystyle \overrightarrow{OP} = \frac{1}{2}p\overrightarrow{OA}+t\overrightarrow{OB} \)
\( \displaystyle \overrightarrow{OP} = p・\frac{1}{2}\overrightarrow{OA}+t\overrightarrow{OB} \)とおけます。
\( \displaystyle \frac{1}{2}\overrightarrow{OA} = \overrightarrow{OE} \)とすると、
\( \displaystyle \frac{1}{2}p≧0 \),$t≧0$,$1≦p+t≦2$、つまり$p≧0$,$t≧0$,$1≦p+t≦2$であり、
\( \overrightarrow{OP} = p\overrightarrow{OE}+t\overrightarrow{OB} \)ということになります。
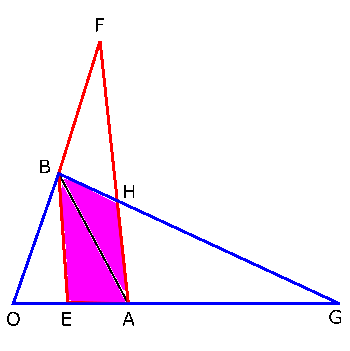
さっきの(2)と同じように考えると、これが表す点$P$が存在する範囲は、\( 2\overrightarrow{OB} = \overrightarrow{OF} \)とすると、右の図でいうと四角形$BEAF$の周と内部(赤い枠線で囲われた部分)ということになります。
次に、$s≧0$,$t≧0$,$s+3t≦3$のときに点$P$が存在する範囲を考えます。
$●●≦1$の形に変形するために、$s+3t≦3$の両辺を3で割ると、\( \displaystyle \frac{1}{3}s+t≦1 \)です。
\( \displaystyle \frac{1}{3}s = q \)とおくと、$s = 3q$なので、
\( \overrightarrow{OP} = 3q\overrightarrow{OA}+t\overrightarrow{OB} \)
\( \overrightarrow{OP} = q・3\overrightarrow{OA}+t\overrightarrow{OB} \)
\( 3\overrightarrow{OA} = \overrightarrow{OG} \)とすると、
$3q≧0$,$t≧0$,$q+t≦1$、つまり$q≧0$,$t≧0$,$q+t≦1$であり、
\( \overrightarrow{OP} = q\overrightarrow{OG}+t\overrightarrow{OB} \)ということになります。
これが表す点$P$が存在する範囲は、さっきの図でいうと$△OGB$の周と内部(青い枠線で囲われた部分)ということになります。
よって、$s≧0$,$t≧0$,$1≦2s+t≦2$,$s+3t≦3$を満たすときに点$P$が存在する範囲は、$AF$と$BG$の交点を$H$とすると、四角形$BEAF$と$△OGB$の2つが重なる部分である四角形$BEAH$(図の紫色で塗られている部分)です。ここの面積を求めればいいわけです。
その面積を求めるために、$△BEA$と$△BAH$に分けて考えます。
$△BEA$について、\( \displaystyle \frac{1}{2}OA = OE \)(=$E$は$OA$の中点)なので、
\( \displaystyle △BEA = \frac{1}{2}△OAB = \frac{1}{2}・6\sqrt{6} = 3\sqrt{6} \)
$△BAH$について考えると、まず$3OA = OG$より、$AG = OG-OA = 3OA-OA = 2OA$なので、
\( △BAG = 2△OAB = 2・6\sqrt{6} = 12\sqrt{6} \)
また、$OF = 2OB$、つまり$B$は$OF$の中点ですから、中点連結定理により、$BE$と$FA$は平行です。
このため、$BE$と$HA$も平行となるため、\( EA:AG = BH:HG \)といえます。
$AG = 2OA$で、\( \displaystyle \frac{1}{2}OA = OE \),つまり$OA = 2OE$なので、$AG = 2・2OE = 4OE$
$EA = OA$なので、\( EA:AG = BH:HG = 1:4 \)
さっき求めた$△BAG$の面積を利用して$△BAH$の面積を求めると、
\( \displaystyle \frac{1}{1+4}△BAG = \frac{1}{5}・12\sqrt{6} = \frac{12\sqrt{6}}{5} \)
よって、四角形$BEAH$の面積は、
\( △BEA+△BAH \)
\( \displaystyle = 3\sqrt{6}+\frac{12\sqrt{6}}{5} = \frac{27\sqrt{6}}{5} \)
(別解)
四角形$BEAH$の面積を、$△BEG$から$△HAG$を引くことで求めるという方法もあります。
さっきの解説にも示したとおり、$AG = 4OE$であり、$E$は$OA$の中点なので$OA = 2OE$です。
そのため、
\( OA:EG \)
\( = 2OE:(EA+AG) \)
\( = 2OE:(OE+4OE) = 2:5 \)
これより、$△BEG$の面積は\( \displaystyle \frac{5}{2}△OAB \)といえます。
そして、さっきの解説のとおり、$BE$//$HA$より$△BEG$と$△HAG$は相似です。その相似比は、
\( EG:AG = 5OE:4OE = 5:4 \)
よって、$△BEG$と$△HAG$の面積比は、\( 5^2:4^2 = 25:16 \)なので、$△HAG$の面積は
\( \displaystyle \frac{16}{25}×\frac{5}{2}△OAB = \frac{8}{5}△OAB \)
よって、四角形$BEAH$の面積は、
\( △BEG-△HAG \)
\( \displaystyle = \frac{5}{2}△OAB-\frac{8}{5}△OAB \)
\( \displaystyle = \frac{9}{10}△OAB \)と表されます。
$△OAB$の面積は(1)より\( 6\sqrt{6} \)ですから、求める面積は
\( \displaystyle \frac{9}{10}・6\sqrt{6} = \frac{27\sqrt{6}}{5} \)
答え.
(1)\( 6\sqrt{6} \)
(2)\( 18\sqrt{6} \)
(3)\( \displaystyle \frac{27\sqrt{6}}{5} \)