この問題のポイント
斜回転した回転体の体積は、軸になる直線との距離を半径にした円の面積を積分したもの!
(1)$l$と$C$を表す式から$y$を消去すると、
\( \displaystyle x = \frac{\sqrt{2}}{4}x^2+\frac{\sqrt{2}}{2} \)
\( 4x = \sqrt{2}x^2+2\sqrt{2} \)
\( \sqrt{2}x^2-4x+2\sqrt{2} = 0 \)
この方程式を解くと、
\( \displaystyle x = \frac{-(-2)±\sqrt{(-2)^2-\sqrt{2}・2\sqrt{2}}}{\sqrt{2}} \)
\( \displaystyle = \frac{2±\sqrt{0}}{\sqrt{2}} \)
\( \displaystyle = \frac{2}{\sqrt{2}} \)
\( = \sqrt{2} \)
もともと$l$は$x≧0$の範囲での半直線ですから、$x$の値はこれを満たしている必要がありますが、\( x = \sqrt{2} \)はこれを満たしています。
$l$の式は\( y = x \)なので、\( x = \sqrt{2} \)のときの$y$座標も\( \sqrt{2} \)です。よって、求める座標は\( (\sqrt{2},\sqrt{2}) \)です。
(2)$l$上の$A(t)$の座標を\( (m,m) \)とします。原点からの距離が$t$ということは、
\( \sqrt{p^2+p^2} = t \)
\( \sqrt{2p^2} = t \)
\( 2p^2 = t^2 \)
\( \displaystyle p^2 = \frac{t^2}{2} \)
$A(t)$の$x$座標は正で、$t≧0$より、\( \displaystyle p = \frac{t}{\sqrt{2}} \)
よって、$A(t)$の座標は\( \displaystyle \left(\frac{t}{\sqrt{2}},\frac{t}{\sqrt{2}}\right) \)となります。
$l$の傾きは1ですから、それに直交する直線の傾きは-1です。なので、この直線を$l_1$とすると、$l_1$の方程式は
\( \displaystyle y-\frac{t}{\sqrt{2}} = -\left(x-\frac{t}{\sqrt{2}}\right) \)
\( \displaystyle y = -\left(x-\frac{t}{\sqrt{2}}\right)+\frac{t}{\sqrt{2}} \)
\( \displaystyle y = -x+\frac{t}{\sqrt{2}}+\frac{t}{\sqrt{2}} \)
\( \displaystyle y = -x+\frac{2t}{\sqrt{2}} \)
\( y = -x+\sqrt{2}t \)
これと$C$が共有点をもつこととなるので、(1)と同様に$y$を消去すると、
\( \displaystyle -x+\sqrt{2}t = \frac{\sqrt{2}}{4}x^2+\frac{\sqrt{2}}{2} \)
\( -4x+4\sqrt{2}t = \sqrt{2}x^2+2\sqrt{2} \)
\( \sqrt{2}x^2+4x+2\sqrt{2}-4\sqrt{2}t = 0 \)
この方程式を解くと、
\( \displaystyle x = \frac{-2±\sqrt{2^2-\sqrt{2}・(2\sqrt{2}-4\sqrt{2}t)}}{\sqrt{2}} \)
\( \displaystyle = \frac{-2±\sqrt{4-4+8t}}{\sqrt{2}} \)
\( \displaystyle = \frac{-2±2\sqrt{2t}}{\sqrt{2}} \)
\( \displaystyle = \frac{\sqrt{2}(-2±2\sqrt{2t})}{2} \)
\( \displaystyle = \frac{-2\sqrt{2}±4\sqrt{t}}{2} \)
\( = -\sqrt{2}±2\sqrt{t} \)
この値を\( y = -x+\sqrt{2}t \)に代入して計算すると、\( y = \sqrt{2}\mp2\sqrt{t}+\sqrt{2}t \)
よって、求める座標は\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \),\( (-\sqrt{2}-2\sqrt{t},\sqrt{2}+2\sqrt{t}+\sqrt{2}t) \)です。
(3)「放物線$C$と半直線$l$および$y$軸とで囲まれた図形」を図で示すと下の図のようになります。さっきの(2)で考えた半直線$l$に直交する直線を$l_1$としています。
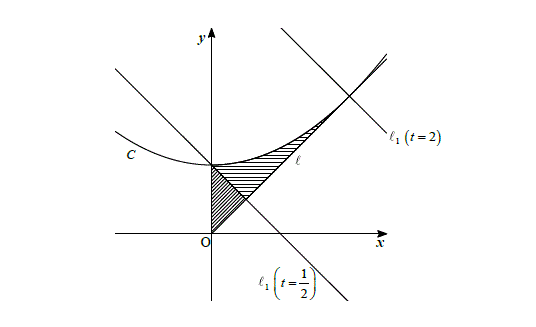
この図を見ると、$l_1$のうち\( \displaystyle t = \frac{1}{2} \)である直線を引くと、該当する図形を2つに分けることができることに気づきます。
ちなみに、なぜ\( \displaystyle t = \frac{1}{2} \)である必要があるかですが、$l_1$の方程式は(2)より\( y = -x+\sqrt{2}t \)ですが、その直線は放物線$C$の頂点\( \displaystyle \left(0,\frac{\sqrt{2}}{2}\right) \)を通るので、\( \displaystyle \sqrt{2}t = \frac{\sqrt{2}}{2} \)であり、これを解くと、\( \displaystyle t = \frac{1}{2} \)となるためです。
さて、上の図の斜線がつけられた部分について、直線$l$上にある$A(t)$の座標は\( \displaystyle \left(\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right) \)ですから、これと放物線$C$の頂点\( \displaystyle \left(0,\frac{\sqrt{2}}{2}\right) \)の距離は、
\( \displaystyle \sqrt{\left(\frac{1}{2\sqrt{2}}\right)^2+\left(\frac{1}{2\sqrt{2}}-\frac{\sqrt{2}}{2}\right)^2} \)
\( \displaystyle = \sqrt{\left(\frac{\sqrt{2}}{4}\right)^2+\left(\frac{\sqrt{2}}{4}-\frac{\sqrt{2}}{2}\right)^2} \)
\( \displaystyle = \sqrt{\frac{1}{8}+\left(-\frac{\sqrt{2}}{4}\right)^2} \)
\( \displaystyle = \sqrt{\frac{1}{8}+\frac{1}{8}} \)
\( \displaystyle = \sqrt{\frac{1}{4}} = \frac{1}{2} \)
\( \displaystyle t = \frac{1}{2} \)、つまり原点からの距離が\( \displaystyle \frac{1}{2} \)ですから、図の斜線がつけられた部分を半直線$l$のまわりに1回転すると、半径が\( \displaystyle \frac{1}{2} \)の円が底面で高さが\( \displaystyle \frac{1}{2} \)である円錐ができることとなります。その体積は、
\( \displaystyle \frac{1}{3}・\left(\frac{1}{2}\right)^2・π・\frac{1}{2} = \frac{1}{24}π \)
次に、図の横線がつけられた部分について考えます。$l_1$と$C$の交点のうち、$x$座標の大きいものは\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \),\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \)です。横線がつけられた部分の回転体の体積は、この点と直線$l$との距離を半径とした円の面積を積分することで求まるはずです。
点と直線の距離の公式を使って求めることもできますが、$A(t)$の座標を(2)で求めています。直線$l$との距離は$A(t)$との距離ともいえますから、\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \),\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \)と$A(t)$との距離を求めると、
\( \displaystyle \small{\sqrt{\left(-\sqrt{2}+2\sqrt{t}-\frac{t}{\sqrt{2}}\right)^2+\left(\sqrt{2}-2\sqrt{t}+\sqrt{2}t-\frac{t}{\sqrt{2}}\right)^2}} \)
これを整理すると、\( (\sqrt{t}-\sqrt{2})^2 \)です。
これを半径にした円の面積を積分します。このときの$t$の範囲は\( \displaystyle \frac{1}{2} \)以上2以下ですから、
\( \displaystyle π\int_\frac{1}{2}^2 (\sqrt{t}-\sqrt{2})^4dt \)
ここで、\( s = \sqrt{t}-\sqrt{2} \)とおくと、両辺を微分すると、\( \displaystyle ds = \frac{1}{2\sqrt{t}}dt \)
\( s = \sqrt{t}-\sqrt{2} \)とおいたので\( \sqrt{t} = s+\sqrt{2} \)だから、
\( \displaystyle ds = \frac{1}{2(s+\sqrt{2})}dt \)
\( \displaystyle ∴\frac{ds}{dt} = 2(s+\sqrt{2}) \)
\( \displaystyle t = \frac{1}{2} \)のとき\( \displaystyle s = -\frac{\sqrt{2}}{2} \),$t = 2$のとき$s = 0$より、置換積分を利用して、
\begin{eqnarray} &&\displaystyle π\int_\frac{1}{2}^2 (\sqrt{t}-\sqrt{2})^4dt\\ &&\displaystyle = π\int_{-\frac{\sqrt{2}}{2}}^0 s^4\frac{ds}{dt}ds\\ &&\displaystyle = π\int_{-\frac{\sqrt{2}}{2}}^0 s^4・2(s+\sqrt{2})ds\\ &&\displaystyle = 2π\int_{-\frac{\sqrt{2}}{2}}^0 (s^5+\sqrt{2}s^4)ds\\ &&\displaystyle = 2π\left[\frac{s^6}{6}+\frac{\sqrt{2}}{5}s^5\right]_{-\frac{\sqrt{2}}{2}}^0\\ &&\displaystyle = 2π\left\{0-\left(\frac{1}{48}-\frac{1}{20}\right)\right\}\\ &&\displaystyle = -\frac{1}{24}π+\frac{1}{10}π \end{eqnarray}
よって、斜線がつけられた部分と横線がつけられた部分の体積をたして、
\( \displaystyle \frac{1}{24}π-\frac{1}{24}π+\frac{1}{10}π = \frac{1}{10}π \)
答え.
(1)
\( (\sqrt{2},\sqrt{2}) \)
(2)
\( (-\sqrt{2}+2\sqrt{t},\sqrt{2}-2\sqrt{t}+\sqrt{2}t) \),\( (-\sqrt{2}-2\sqrt{t},\sqrt{2}+2\sqrt{t}+\sqrt{2}t) \)
(3)
\( \displaystyle \frac{1}{10}π \)