この問題のポイント
1のn乗根はcos2k$π$/n+isin2k$π$/nと表せて、複素数平面上ではすべて半径1の円周上にある!
(1)\( \displaystyle \frac{2π}{7} \)は7倍すると$2π$となるので1周して戻ってくることになります。よって、ド・モアブルの定理より、
\begin{eqnarray} &&\displaystyle z^7 = \left(\cos{\frac{2π}{7}}+i\sin{\frac{2π}{7}}\right)^7\\ &&\displaystyle = \cos{\left(7・\frac{2π}{7}\right)}+i\sin{\left(7・\frac{2π}{7}\right)}\\ &&= \cos{2π}+i\sin{2π}\\ &&= 1 \end{eqnarray}
\( z^7 = 1 \)より、\( z^7-1 = 0 \)
$z = 1$のとき、この方程式は成り立ちますから、因数定理より、$(z-1)$で因数分解できます。それで因数分解すると、
\( (z-1)(z^6+z^5+z^4+z^3+z^2+z+1) = 0 \)
しかし、もともと問題文で\( \displaystyle z = \cos{\frac{2π}{7}}+i\sin{\frac{2π}{7}} \)とありましたから、実際は\( z \neq 1 \)なので、
\( z^6+z^5+z^4+z^3+z^2+z+1 = 0 \)
\( ∴z^6+z^5+z^4+z^3+z^2+z = -1 \)
(2)\( z^7 = 1 \)より、$z$は1の7乗根です。一般的に、$z$が1の$n$乗根のとき、$z$は\( \displaystyle z = \cos{\frac{2kπ}{n}}+i\sin{\frac{2kπ}{n}} \)($k$は1から$n-1$までの整数)とあらわすことができます。そして、ド・モアブルの定理からいえば、$z$を2乗,3乗,…とすれば偏角は2倍,3倍,…となります。
さらに、共役複素数を考えると、\( \displaystyle z = \cos{\frac{2π}{7}}+i\sin{\frac{2π}{7}} \)についてであれば、
\( \displaystyle \overline{z} = \cos{\frac{2π}{7}}-i\sin{\frac{2π}{7}} \)
\( \displaystyle = \cos{\left(-\frac{2π}{7}\right)}+i\sin{\left(-\frac{2π}{7}\right)} \)
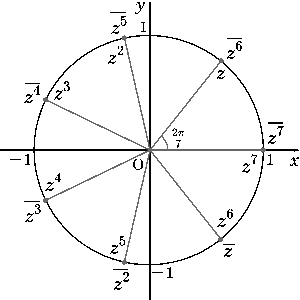
このように変形できますので、共役複素数を2乗,3乗,…とすれば偏角は反対まわりに2倍,3倍,…となります。よって、$z$から$z^6$までについて共役複素数をふくめてあらわすと右の図のようになります。このように、1の$n$乗根は、複素数平面では半径が1の円の上に等間隔に存在し、共役複素数は実軸と対称の位置どうしになります。
よって、\( \overline{z} = z^6 \),\( \overline{z^2} = z^5 \),\( \overline{z^4} = z^3 \)なので、$α = z+z^2+z^4$のとき、
\( \overline{α} = \overline{z}+\overline{z^2}+\overline{z^4} = z^6+z^5+z^3 \)
\( ∴α+\overline{α} \)
\( = z+z^2+z^4+z^6+z^5+z^3 \)
\( = z+z^2+z^3+z^4+z^5+z^6 = -1 \)(∵(1)より)
\( α\overline{α} \)
\( = (z+z^2+z^4)(z^6+z^5+z^3) \)
\( = z^7+z^6+z^4+z^8+z^7+z^5+z^{10}+z^9+z^7 \)
\( = z^7+z^6+z^4+z^7・z+z^7+z^5+z^7・z^3+z^7・z^2+z^7 \)
\( = 1+z^6+z^4+z+1+z^5+z^3+z^2+1 \)
\( = 3+z+z^2+z^3+z^4+z^5+z^6 \)
= 3-1 = 2(∵(1)より)
\( α\overline{α} \)
\( = (z+z^2+z^4)(z^6+z^5+z^3) \)
\( = z^7+z^6+z^4+z^8+z^7+z^5+z^{10}+z^9+z^7 \)
\( = z^7+z^6+z^4+z^7・z+z^7 \)
\( ~~~~+z^5+z^7・z^3+z^7・z^2+z^7 \)
\( = 1+z^6+z^4+z+1+z^5+z^3+z^2+1 \)
\( = 3+z+z^2+z^3+z^4+z^5+z^6 \)
= 3-1 = 2(∵(1)より)
最後に$α$を求めますが、\( α+\overline{α} = -1 \),\( α\overline{α} = 2 \)と求まりましたから、$α$,\( \overline{α} \)を方程式の解とみなすと、解と係数の関係より、この2つは
\( x^2+x+2 = 0 \)の解であるとわかります。
この方程式を解くと、\( \displaystyle x = \frac{-1±\sqrt{7}i}{2} \)
ここで、$α = z+z^2+z^4$なので、$α$の虚部は\( \displaystyle \sin{\frac{2π}{7}}+\sin{\frac{4π}{7}}+\sin{\frac{8π}{7}} \)
そして、\( \displaystyle \sin{\frac{8π}{7}} = -\sin{\frac{6π}{7}} \)であり、\( \displaystyle \sin{\frac{6π}{7}} \)より\( \displaystyle \sin{\frac{4π}{7}} \)のほうが絶対値は大きいので、\( \displaystyle \sin{\frac{2π}{7}}+\sin{\frac{4π}{7}}+\sin{\frac{8π}{7}}>0 \)
つまり、$α$の虚部は正ということになるので、\( \displaystyle α = \frac{-1+\sqrt{7}i}{2} \)
(3)さっきの(2)の解説にあった図より、方程式$x^7 = 1$、つまり$x^7-1 = 0$の解は
$x$ = $1$,$z$,$z^2$,$z^3$,$z^4$,$z^5$,$z^6$の7つとわかります。
よって、因数定理より、
\( x^7-1 \)
\( = (x-1)(x^6+x^5+x^4+x^3+x^2+x+1) \)
\( = (x-1)(x-z)(x-z^2)(x-z^3)…(x-z^6) \)
これより、次の式が成り立ちます。
\( \small{x^6+x^5+x^4+x^3+x^2+x+1} \)
\( \small{= (x-z)(x-z^2)(x-z^3)(x-z^4)(x-z^5)(x-z^6)} \)
この式に$x = 1$を代入すると、
\( \small{1^6+1^5+1^4+1^3+1^2+1+1} \)
\( \small{= (1-z)(1-z^2)(1-z^3)(1-z^4)(1-z^5)(1-z^6)} \)
これより、\( \small{(1-z)(1-z^2)(1-z^3)(1-z^4)(1-z^5)(1-z^6) = 7} \)となります。
答え.
(1)
-1
(2)
\( α+\overline{α} = -1 \),\( α\overline{α} = 2 \)
\( \displaystyle α = \frac{-1+\sqrt{7}i}{2} \)
(3)
7