この問題のポイント
媒介変数表示された関数を積分するときは、媒介変数で置換積分する!
xとyが1対1で対応していない関数のグラフの面積は上側と下側に分けて積分する!
(1)\( x = 3\cos{t}-\cos{3t} \)なので、
\( \displaystyle \frac{dx}{dt} = -3\sin{t}+3\sin{3t} \)
\( = 3(\sin{3t}-\sin{t}) \)
三角関数の和積の公式を使って変形します。
\( \displaystyle 3・2\cos{\frac{3t+t}{2}}\sin{\frac{3t-t}{2}} \)
\( = 6\cos{2t}\sin{t} \)
\( \displaystyle ∴\frac{dx}{dt} = 6\cos{2t}\sin{t} \)
\( y = 3\sin{t}-\sin{3t} \)なので、
\( \displaystyle \frac{dy}{dt} = 3\cos{t}-3\cos{3t} \)
\( = -3(\cos{3t}-\cos{t}) \)
\( \displaystyle \frac{dx}{dt} \)と同じように、三角関数の和積の公式を使って変形します。
\( \displaystyle -3・\left(-2\sin{\frac{3t+t}{2}}\sin{\frac{3t-t}{2}}\right) \)
\( = 6\sin{2t}\sin{t} \)
\( \displaystyle ∴\frac{dy}{dt} = 6\sin{2t}\sin{t} \)
ここで、\( \displaystyle 0≦t≦\frac{π}{2} \)において、\( \displaystyle \frac{dx}{dt} = 0 \)となるのは、\( 6\cos{2t}\sin{t} = 0 \)のときなので、\( \displaystyle t = 0,\frac{π}{4} \)のときです。
そして、\( \displaystyle \frac{dy}{dt} = 0 \)となるのは、\( 6\sin{2t}\sin{t} = 0 \)のときなので、\( \displaystyle t = 0,\frac{π}{2} \)のときです。
よって、増減表は下のようになります。
| $t$ | 0 | … | \( \displaystyle \frac{π}{4} \) | … | \( \displaystyle \frac{π}{2} \) |
| \( \displaystyle \frac{dx}{dt} \) | 0 | + | 0 | - | |
| $x$ | 2 | → | \( 2\sqrt{2} \) | ← | 0 |
| \( \displaystyle \frac{dy}{dt} \) | 0 | + | + | 0 | |
| $y$ | 0 | ↑ | \( \sqrt{2} \) | ↑ | 4 |
| \( (x,y) \) | (2,0) | ↗ | \( (2\sqrt{2},\sqrt{2}) \) | ↖ | (0,4) |
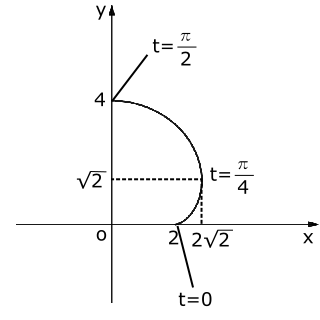
よって、$C$の概形は右の図のようになります。
媒介変数で示された関数は一見、どのようなグラフの形になるのかつかみにくいです。なので、グラフを描く際は、このように\( \displaystyle \frac{dx}{dt} \)や\( \displaystyle \frac{dy}{dt} \)を求めて\( \displaystyle \frac{dx}{dt} \)や\( \displaystyle \frac{dy}{dt} \)が0になるところを境に増減がどうなるのか調べることが必要になります。
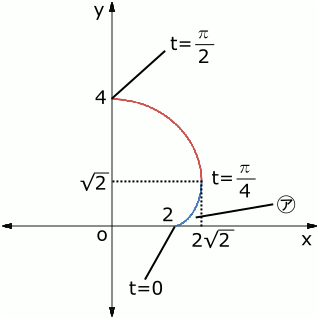
(2)グラフについて、囲まれた部分の面積を求めるわけなので積分をすればいいということになります。この関数について、$x$がとりうる値の範囲は\( 0≦x≦2\sqrt{2} \)ですから、
\( \displaystyle \int_0^{2\sqrt{2}} ydx \)
で計算すればいいと思ったかもしれません。
しかし、グラフをよく見ると、途中で折り返しがある曲線になっています。よって、この積分で計算をしてしまうと、㋐の部分まで含んだ面積が求まってしまいます。「$x$がこの値なら$y$は必ずこの値」と$x$と$y$が完全に1対1に対応している形ではないからこのような曲線になっているわけですが、このように$x$と$y$が完全に1対1に対応しているわけではないグラフの面積は折り返す前と後でグラフを分けて考える必要があります。
そこで、\( \displaystyle 0≦t≦\frac{π}{4} \)のときの曲線を$y_1$(図の青色の部分)、\( \displaystyle \frac{π}{4}<t≦\frac{π}{2} \)のときの曲線を$y_2$(図の赤色の部分)とおきます。すると、求める面積は、
\( \displaystyle \int_0^{2\sqrt{2}} y_2dx-\int_0^2 y_1dx \)
と考えられます。ところが、$y_1$も$y_2$ももともとは$y$のことをあらわしますが、$y$は媒介変数の$t$の式で表されていました。$t$の式を$x$で積分することはできないはずです。
では$dx$ではなく$dt$にすればよいと思われたかもしれませんが、グラフの横軸は$x$ですから、勝手に変えてしまうと横軸を勝手に変えたことになってしまい、面積が正しく求まりません。なので、媒介変数表示された関数の面積は媒介変数で置換積分して求めます。この問題の場合であれば、$t$で置換積分します。
さっきの(1)で求めたとおり、\( \displaystyle \frac{dx}{dt} = -3\sin{t}+3\sin{3t} \)より、
\( dx = (-3\sin{t}+3\sin{3t})dt \)
\begin{eqnarray} &&\small{∴\int_0^{2\sqrt{2}} y_2dx-\int_0^2 y_1dx}\\ &&\small{= \int_{\frac{π}{2}}^{\frac{π}{4}} y_2・(-3\sin{t}+3\sin{3t})dt-\int_0^{\frac{π}{4}} y_1・(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= \int_{\frac{π}{2}}^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt-\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\int_{\frac{π}{4}}^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt-\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\left\{\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt+\int_{\frac{π}{4}}^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt\right\}}\\ &&\small{= -\int_0^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\int_0^{\frac{π}{2}} (-9\sin^2{t}+12\sin{3t}\sin{t}-3\sin^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} (3\sin^2{t}-4\sin{3t}\sin{t}+\sin^2{3t})dt}\\ \end{eqnarray}
\begin{eqnarray} &&\small{∴\int_0^{2\sqrt{2}} y_2dx-\int_0^2 y_1dx}\\ &&\small{= \int_{\frac{π}{2}}^{\frac{π}{4}} y_2・(-3\sin{t}+3\sin{3t})dt}\\ &&\small{~~~~-\int_0^{\frac{π}{4}} y_1・(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= \int_{\frac{π}{2}}^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{~~~~-\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\int_{\frac{π}{4}}^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{~~~~-\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\left\{\int_0^{\frac{π}{4}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt\right.}\\ &&\small{~~~~\left.+\int_{\frac{π}{4}}^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt\right\}}\\ &&\small{= -\int_0^{\frac{π}{2}} (3\sin{t}-\sin{3t})(-3\sin{t}+3\sin{3t})dt}\\ &&\small{= -\int_0^{\frac{π}{2}} (-9\sin^2{t}+12\sin{3t}\sin{t}-3\sin^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} (3\sin^2{t}-4\sin{3t}\sin{t}+\sin^2{3t})dt}\\ \end{eqnarray}
\( \sin^2{t} \)や\( \sin^2{3t} \)については半角の公式、\( \sin{3t}\sin{t} \)については積和の公式を使って変形します。係数に三角関数が使われていると積分の計算がしにくいのでそれを解消し、\( \cos{} \)だけの足し算の形にしていくためです。
\begin{eqnarray} &&\small{3\int_0^{\frac{π}{2}} (3\sin^2{t}-4\sin{3t}\sin{t}+\sin^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left\{3・\frac{1-\cos{2t}}{2}+2(\cos{4t}-\cos{2t})+\frac{1-\cos{6t}}{2}\right\}dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left(-\frac{1}{2}\cos{6t}+2\cos{4t}-\frac{7}{2}\cos{2t}+2\right)dt}\\ &&\small{= \frac{3}{2}\int_0^{\frac{π}{2}} (-\cos{6t}+4\cos{4t}-7\cos{2t}+4)dt}\\ &&\small{= \frac{3}{2}\left[-\frac{1}{6}\sin{6t}+\sin{4t}-\frac{7}{2}\sin{2t}+4t\right]_0^{\frac{π}{2}}}\\ &&\small{= \frac{3}{2}・2π = 3π}\\ \end{eqnarray}
\begin{eqnarray} &&\small{3\int_0^{\frac{π}{2}} (3\sin^2{t}-4\sin{3t}\sin{t}+\sin^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left\{3・\frac{1-\cos{2t}}{2}+2(\cos{4t}-\cos{2t})\right.}\\ &&\small{~~~~\left.+\frac{1-\cos{6t}}{2}\right\}dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left(-\frac{1}{2}\cos{6t}+2\cos{4t}-\frac{7}{2}\cos{2t}+2\right)dt}\\ &&\small{= \frac{3}{2}\int_0^{\frac{π}{2}} (-\cos{6t}+4\cos{4t}-7\cos{2t}+4)dt}\\ &&\small{= \frac{3}{2}\left[-\frac{1}{6}\sin{6t}+\sin{4t}-\frac{7}{2}\sin{2t}+4t\right]_0^{\frac{π}{2}}}\\ &&\small{= \frac{3}{2}・2π = 3π}\\ \end{eqnarray}
(別解)
$x$軸方向にではなく、$y$軸方向に定積分すれば、さっきのように「折り返しがあるからその分の面積を引く」ということを考えずに解くことができます。$y$の範囲は\( 0≦y≦4 \)なので、
\( \displaystyle \int_0^4 xdy \)とおけます。
もちろん、この積分でも、$x$や$y$は$t$で表されているだけでしたから、さっきの$x$軸方向に積分したときと同じく、置換積分をしなければいけません。
\( \displaystyle \frac{dy}{dt} = 3\cos{t}-3\cos{3t} \)と(1)で求めたはずなので、\( dy = (3\cos{t}-3\cos{3t})dt \)
\begin{eqnarray} &&\small{∴\int_0^4 xdy}\\ &&\small{= \int_0^{\frac{π}{2}} x・(3\cos{t}-3\cos{3t})dt}\\ &&\small{= \int_0^{\frac{π}{2}} (3\cos{t}-\cos{3t})(3\cos{t}-3\cos{3t})dt}\\ &&\small{= \int_0^{\frac{π}{2}} (9\cos^2{t}-12\cos{3t}\cos{t}+3\cos^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} (3\cos^2{t}-4\cos{3t}\cos{t}+\cos^2{3t})dt}\\ \end{eqnarray}
これも半角の公式や積和の公式を使って変形していきます。
\begin{eqnarray} &&\small{3\int_0^{\frac{π}{2}} (3\cos^2{t}-4\cos{3t}\cos{t}+\cos^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left\{3・\frac{1+\cos{2t}}{2}-2(\cos{4t}+\cos{2t})+\frac{1+\cos{6t}}{2}\right\}dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left(\frac{1}{2}\cos{6t}-2\cos{4t}-\frac{1}{2}\cos{2t}+2\right)dt}\\ &&\small{= \frac{3}{2}\int_0^{\frac{π}{2}} (\cos{6t}-4\cos{4t}-\cos{2t}+4)dt}\\ &&\small{= \frac{3}{2}\left[\frac{1}{6}\sin{6t}-\sin{4t}-\frac{1}{2}\sin{2t}+4t\right]_0^{\frac{π}{2}}}\\ &&\small{= \frac{3}{2}・2π = 3π}\\ \end{eqnarray}
\begin{eqnarray} &&\small{3\int_0^{\frac{π}{2}} (3\cos^2{t}-4\cos{3t}\cos{t}+\cos^2{3t})dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left\{3・\frac{1+\cos{2t}}{2}-2(\cos{4t}+\cos{2t})\right.}\\ &&\small{~~~~\left.+\frac{1+\cos{6t}}{2}\right\}dt}\\ &&\small{= 3\int_0^{\frac{π}{2}} \left(\frac{1}{2}\cos{6t}-2\cos{4t}-\frac{1}{2}\cos{2t}+2\right)dt}\\ &&\small{= \frac{3}{2}\int_0^{\frac{π}{2}} (\cos{6t}-4\cos{4t}-\cos{2t}+4)dt}\\ &&\small{= \frac{3}{2}\left[\frac{1}{6}\sin{6t}-\sin{4t}-\frac{1}{2}\sin{2t}+4t\right]_0^{\frac{π}{2}}}\\ &&\small{= \frac{3}{2}・2π = 3π}\\ \end{eqnarray}
答え.
(1)
\( \displaystyle \frac{dx}{dt} = 6\cos{2t}\sin{t} \)
\( \displaystyle \frac{dy}{dt} = 6\sin{2t}\sin{t} \)
($C$の概形は上の解説参照)
(2)
$3π$