この問題のポイント
双曲線の定義と標準形の方程式、焦点や漸近線の方程式との関係を理解しよう!
(1)楕円\( \displaystyle \frac{x^2}{9}+\frac{y^2}{5} = 1 \)の焦点をまずはっきりとさせないといけません。楕円\( \displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \)の焦点は\( (-\sqrt{a^2-b^2},0) \)、\( (\sqrt{a^2-b^2},0) \)の2つでしたから、$F$は\( (\sqrt{9-5},0) \)つまり(2,0)、$F'$は\( (-\sqrt{9-5},0) \)つまり(-2,0)です。
$C_2$は双曲線ですが、まず双曲線とはどのようなものなのか、その定義や方程式を確認しましょう。
双曲線の定義
双曲線とはある2点からの距離の差が一定となる点の軌跡のことで、そのときの2点を焦点という。
双曲線の標準形の方程式
焦点が$x$軸上にあるときの双曲線(横向き)の方程式は
\( \displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2} = 1 \)(\( a>0,b>0 \))
このとき、
焦点の座標は\( (-\sqrt{a^2+b^2},0) \)と\( (\sqrt{a^2+b^2},0) \)の2つで、焦点からの距離の差は$2a$
漸近線の方程式は\( \displaystyle \frac{x}{a}+\frac{y}{b} = 0 \)と\( \displaystyle \frac{x}{a}-\frac{y}{b} = 0 \)(つまり、\( \displaystyle y = ±\frac{b}{a}x \)の2本がある)
焦点が$y$軸上にあるときの双曲線(縦向き)の方程式は
\( \displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2} = -1 \)(\( a>0,b>0 \))
このとき、
焦点の座標は\( (0,-\sqrt{a^2+b^2}) \)と\( (0,\sqrt{a^2+b^2}) \)の2つで、焦点からの距離の差は$2b$
漸近線の方程式は\( \displaystyle \frac{x}{a}+\frac{y}{b} = 0 \)と\( \displaystyle \frac{x}{a}-\frac{y}{b} = 0 \)(つまり、\( \displaystyle y = ±\frac{b}{a}x \)の2本がある)
$C_2$の焦点は$C_1$と同じ(2,0)と(-2,0)です。$x$軸上の点ですから、$C_2$の方程式を\( \displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2} = 1 \)とおくと、\( \sqrt{a^2+b^2} = 2 \)とおけるので、
\( a^2+b^2 = 4 \)…①
そして、漸近線については\( y = ±mx \)の2本とわかっているので、\( \displaystyle \frac{b}{a} = m \)とおけるので、
\( b = am \)…②
②を①に代入して、
\( a^2+(am)^2 = 4 \)
\( a^2+a^2m^2 = 4 \)
\( (1+m^2)a^2 = 4 \)
\( \displaystyle a^2 = \frac{4}{1+m^2} \)…③
②より\( b^2 = a^2m^2 \)より、③をこれに代入して、
\( \displaystyle b^2 = \frac{4m^2}{1+m^2} \)
これより、$C_2$の方程式は、\( \displaystyle \frac{x^2}{\frac{4}{1+m^2}}-\frac{y^2}{\frac{4m^2}{1+m^2}} = 1 \)
つまり、\( \displaystyle x^2÷\frac{4}{1+m^2}-y^2÷\frac{4m^2}{1+m^2} = 1 \)より、
\( \displaystyle \frac{1+m^2}{4}x^2-\frac{1+m^2}{4m^2}y^2 = 1 \)
(2)$P$は双曲線$C_2$上の点で、この双曲線の焦点は$x$軸上にありました。よって、$FP$と$F'P$の関係について、(1)の赤枠内の説明のとおり、この関係が成り立ちます。
\( \displaystyle F'P-FP = 2\sqrt{\frac{4}{1+m^2}} \)
つまり、\( \displaystyle F'P-FP = 2・\frac{2}{\sqrt{1+m^2}} = \frac{4}{\sqrt{1+m^2}} \)…④
さらに、$P$は楕円$C_1$上の点でもあります。楕円では焦点からの距離の和が一定($2a$で一定)で、この式が成り立ちます。
\( F'P+FP = 2・3 = 6 \)…⑤
④と⑤をたすと、\( \displaystyle 2F'P = 6+\frac{4}{\sqrt{1+m^2}} \)
\( \displaystyle ∴F'P = 3+\frac{2}{\sqrt{1+m^2}} \)
⑤から④をひくと、\( \displaystyle 2FP = 6-\frac{4}{\sqrt{1+m^2}} \)
\( \displaystyle ∴FP = 3-\frac{2}{\sqrt{1+m^2}} \)
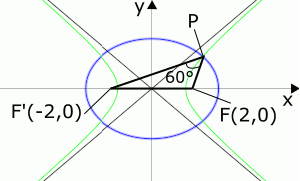
(3)問題文に書かれていることを図にすると右のとおりとなります。青色の線で描かれたものが楕円$C_1$,緑色の線で描かれたものが双曲線$C_2$,黒くて細い直線が$C_2$の漸近線です。
$∠F'PF$ = 60°となったときの$△F'PF$に着目してみると、$F$,$F'$の座標はわかっているのですから、$FF'$ = 4です。そして、(2)にて$FP$と$F'P$について$m$を用いて表しました。
これより、$△F'PF$について余弦定理より、
\( FF'^2 = F'P^2+FP^2-2・F'P・FP・\cos{60°} \)
\( \displaystyle \frac{2}{\sqrt{1+m^2}} = M \)とすると、次のような式になります。
\begin{eqnarray} &&\small{\displaystyle 16 = (3+M)^2+(3-M)^2-2(3+M)(3-M)・\frac{1}{2}}\\ &&\small{16 = 9+6M+M^2+9-6M+M^2-(9-M^2)}\\ &&\small{3M^2+9 = 16}\\ &&\small{3M^2 = 7} \end{eqnarray}
よって、\( \displaystyle M^2 = \frac{7}{3} \)より、\( \displaystyle \frac{4}{1+m^2} = \frac{7}{3} \)ですから、
\( 7(1+m^2) = 12 \)
\( 7m^2 = 5 \)より、\( \displaystyle m^2 = \frac{5}{7} \)
問題文より$m$は正の実数なので、
\( \displaystyle m = \sqrt{\frac{5}{7}} = \frac{\sqrt{35}}{7} \)
答え.
(1)\( \displaystyle \frac{1+m^2}{4}x^2-\frac{1+m^2}{4m^2}y^2 = 1 \)
(2)\( \displaystyle FP = 3-\frac{2}{\sqrt{1+m^2}} \),\( \displaystyle F'P = 3+\frac{2}{\sqrt{1+m^2}} \)
(3)\( \displaystyle m = \frac{\sqrt{35}}{7} \)