この問題のポイント
x座標がaの点における接線の傾きはf'(a)
法線の傾きは-1/f'(a)
(1)\( y = xe^x+1 \)の\( x = 1 \)に対応する点とは\( (1,e+1) \)です。まず接線についてですが、数学Ⅱで学習したとおり、関数$y = f(a)$上で$x$座標が$a$である点における接線の傾きは$f'(a)$でしたね?
\( y = xe^x+1 \)を微分すると\( y' = (x+1)e^x \)なので、\( (1,e+1) \)における接線の傾きは\( (1+1)e^1 = 2e \)です。
そして、点\( (a,b) \)を通り、傾きが$m$の直線の方程式は$y-b = m(x-a)$と表せるのですから、\( (1,e+1) \)における接線の方程式は、
\( y-(e+1) = 2e(x-1) \)
\( y = 2ex-2e+e+1 \)
\( ∴y = 2ex-e+1 \)
そして法線についてですが、法線とは接線と垂直に交わる直線のことです。2直線が垂直に交わっているとき、その2本の直線の傾きどうしをかけあわせると-1になるんですから、法線の傾きは\( \displaystyle -\frac{1}{f'(a)} \)と表せます。
よって、\( (1,e+1) \)における法線の傾きは\( \displaystyle -\frac{1}{(1+1)e^1} = -\frac{1}{2e} \)なので、法線の方程式は、
\( \displaystyle y-(e+1) = -\frac{1}{2e}(x-1) \)
\( \displaystyle ∴y = -\frac{1}{2e}x+\frac{1}{2e}+e+1 \)
(2)曲線の方程式がさっきのように$y$ = …の形ではなく、$x$,$y$の方程式として表されています。こういうときは方程式を$x$で微分して導関数$y'$を求めていきます。
この問題の場合は\( x^2+2xy-2x+y-1 = 0 \)…Aを$x$で微分するわけですが、$2xy$の部分は積の微分となることに注意しましょう。つまり、
\( (2xy)' = 2(x)'y+2x(y)' \)となるので、Aを$x$で微分すると、
\( \displaystyle 2x+2y+2x・\frac{dy}{dx}-2+\frac{dy}{dx} = 0 \)
\( \displaystyle (2x+1)\frac{dy}{dx} = -2x-2y+2 \)
よって、
\( \displaystyle \frac{dy}{dx} = \frac{-2x-2y+2}{2x+1} \)
\( \displaystyle = -\frac{2x+2y-2}{2x+1} \)(\( \displaystyle x \neq -\frac{1}{2} \))
これで\( \displaystyle \frac{dy}{dx} \)、つまり微分したものが求まりましたので、これを使えば接線の傾きを求めることができます。\( \displaystyle \frac{dy}{dx} \)の式に$x = 0$,$y = 1$を代入すると、
\( \displaystyle \frac{dy}{dx} = -\frac{2・0+2・1-2}{2・0+1} \)
\( \displaystyle = -\frac{0}{1} = 0 \)
これより、点(0,1)における接線の傾きは0より、接線の方程式は\( y = 1 \)です。
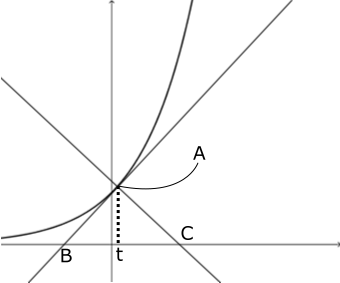
(3)① 接点の座標がわからないと接線を考えることができませんから、点$A$の座標を\( (t,e^t) \)とおきます。すると、\( y' = e^x \)より、接線の傾きは$e^t$とおけますから、接線の方程式は、
\( y-e^t = e^t(x-t) \)
これより、点$B$の座標について、$y$座標は0なので
\( -e^t = e^t(x-t) \)
という方程式が成り立ちますから、\( x-t = -1 \)となるので、\( x = t-1 \)より\( B(t-1,0) \)
そして、法線の傾きは\( \displaystyle -\frac{1}{e^t} \)とわかりますから、法線の方程式は、
\( \displaystyle y-e^t = -\frac{1}{e^t}(x-t) \)
これより、点$C$の座標について、$y$座標は0なので
\( \displaystyle -e^t = -\frac{1}{e^t}(x-t) \)
という方程式が成り立ちますから、\( \displaystyle x-t = e^{2t} \)となるので、\( x = e^{2t}+t \)より\( C(e^{2t}+t,0) \)
図より、$△ABC$は底辺が$BC$,高さが点$A$の$y$座標の値に等しいので、面積は、
\( \displaystyle \frac{1}{2}\{e^{2t}+t-(t-1)\}×e^t \)
\( \displaystyle = \frac{1}{2}e^t(e^{2t}+1) \)
\( \displaystyle = \frac{1}{2}e^{3t}+\frac{1}{2}e^t \)
これが5なので、\( \displaystyle \frac{1}{2}e^{3t}+\frac{1}{2}e^t = 5 \)
\( e^{3t}+e^t = 10 \)
$e^t = X$とすると、\( X^3+X = 10 \)より、\( (X-2)(X^2+2X+5) = 0 \)
\( X^2+2X+5 = 0 \)の解はないので、$X = 2$
よって、$e^t = 2$より、\( t = \log 2 \)
\( A(t,e^t) \)とおいていたので、これを代入して、\( A(\log 2,2) \)
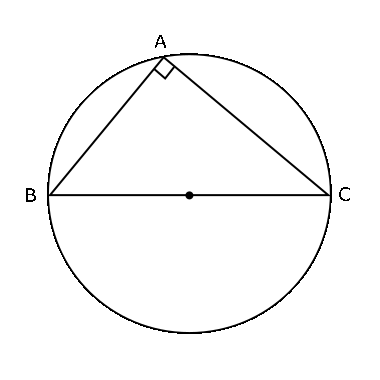
② 接線と法線は垂直に交わるんですから、$△ABC$において$∠A$ = 90°です。ということは、$△ABC$は直角三角形ですから、これの外接円は右の図のように$BC$を直径とする円ということになります。よって、$△ABC$の外心は$BC$の中点です。
さっきの①で\( t = \log 2 \)と求めたので、$B$の座標は\( B(\log 2-1,0) \)
$C$の座標は\( C(4+\log 2,0) \)
よって、その中点は
\( \displaystyle \left(\frac{\log 2-1+4+\log 2}{2},0\right) \)
つまり\( \displaystyle \left(\log 2+\frac{3}{2},0\right) \)
これが外心の座標です。
答え.
(1)
接線…\( y = 2ex-e+1 \)
法線…\( \displaystyle y = -\frac{1}{2e}x+\frac{1}{2e}+e+1 \)
(2)
\( y = 1 \)
(3)
① \( A(\log 2,2) \)
② \( \displaystyle \left(\log 2+\frac{3}{2},0\right) \)