この問題のポイント
楕円の定義と方程式を理解しよう!
楕円は円をy軸方向にa分のb倍引き伸ばしたものということで面積を考える!
(1)問題文の条件より、\( AQ = PQ \)
もともと$Q$は$OP$上の点ですから、それとの関連をもとに式を変形すると、\( OQ+AQ = OQ+PQ \)
\( ∴OQ+AQ = OP = 4 \)
つまり、$Q$は2点$O$,$A$からの距離の和が4で一定であるということになります。このような点は楕円を描きます。ここで、楕円の定義や方程式を確認しておきましょう。
楕円の定義
楕円とは$AP+BP$が一定となる点$P$の軌跡のことで、このときの$A$,$B$のことを焦点という。
楕円の方程式
\( AP+BP = 2a \)とし、楕円の中心を原点とすると、楕円の方程式は
\( \displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \)(\( a>b>0 \))
このとき、
焦点の座標\( A(-\sqrt{a^2-b^2},0) \)、\( B(\sqrt{a^2-b^2},0) \)
長軸の長さは$2a$,短軸の長さは$2b$
\( b>a>0 \)の場合は、焦点は$y$座標上にあり、縦長の楕円になる。
そのとき、
焦点の座標\( A(0,\sqrt{b^2-a^2}) \)、\( B(0,-\sqrt{b^2-a^2}) \)
長軸の長さは$2a$,短軸の長さは$2b$
この問題では、$Q$が描く楕円の焦点は原点$O$と$A(2,0)$で、\( OQ+AQ = 4 \)です。そうなると、楕円の中心が(1,0)となるので、さっきの楕円の方程式が考えられるように、中心を原点にするために、いったん楕円を$x$軸方向に-1(つまり、左に1)ずらして考えましょう。
すると、焦点は(-1,0)と(1,0)となります。長軸の長さは4で$2a = 4$より、$a = 2$だから、$b$の値は、
\( \sqrt{2^2-b^2} = 1 \)
\( 4-b^2 = 1 \)
\( b^2 = 3 \)
\( b>0 \)より、\( b = \sqrt{3} \)
よって、楕円の方程式は、
\( \displaystyle \frac{x^2}{2^2}+\frac{y^2}{(\sqrt{3})^2} = 1 \)
\( \displaystyle ∴\frac{x^2}{4}+\frac{y^2}{3} = 1 \)
そして、この楕円はもともと$x$軸方向にずらして考えられていたのですから、$x$軸方向に1(つまり、右に1)ずらして位置をもとに戻します。$x$のところに$x-1$を代入して、
\( \displaystyle \frac{(x-1)^2}{4}+\frac{y^2}{3} = 1 \)
これが求める方程式です。
(2)(1)で求めた方程式に\( x = 0 \)を代入して、
\( \displaystyle \frac{(-1)^2}{4}+\frac{y^2}{3} = 1 \)
\( \displaystyle \frac{y^2}{3} = \frac{3}{4} \)
\( \displaystyle y^2 = \frac{9}{4} \)
\( \displaystyle y = ±\frac{3}{2} \)
\( d>0 \)なので、\( \displaystyle d = \frac{3}{2} \)
次に、面積について考えなければなりませんが、楕円というのは、もともと円だった図形を横に引き伸ばしてできた図形です。この前提に立つと、楕円について次のようにいうことができます。
\( \displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \)であらわされる楕円は、円\( x^2+y^2 = a^2 \)を$y$軸方向に\( \displaystyle \frac{b}{a} \)倍に拡大したもの
そして、楕円の面積は$πab$となる。
(証明)
\( \displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \)の両辺を$a^2$倍すると、
\( \displaystyle x^2+\left(\frac{a}{b}y\right)^2 = a^2 \)となる。
よって、円\( x^2+y^2 = a^2 \)を$y$軸方向に\( \displaystyle \frac{b}{a} \)倍に拡大したものといえる。
図形を\( \displaystyle \frac{b}{a} \)倍に拡大すると面積も\( \displaystyle \frac{b}{a} \)倍されるので、楕円の面積は、
\( \displaystyle πa^2×\frac{b}{a} = πab \)
よって、この問題の楕円も、もともとの円を\( \displaystyle \frac{\sqrt{3}}{2} \)倍にしたといえます。
ちなみに、「もともとの円」とは、上の赤枠にある内容から考えて、\( (x-1)^2+y^2 = 4 \)です。その円と楕円$D$の関係はこのようになるわけです。
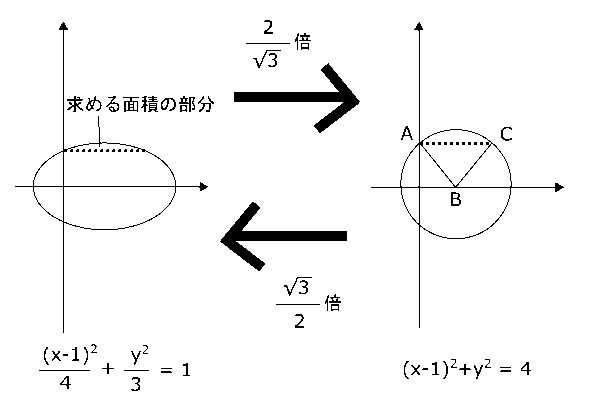
この図の右側のほうで考えてみて、求める面積を考えてみましょう。ただし、右側のほうは楕円を$y$軸方向に加工してつくられたものなので、$d$の値などは変わっています。そこで、面積を求めるうえで重要な点$A$,$B$,$C$の座標をまずは確認します。
$A$…
\( x = 0 \)を\( (x-1)^2+y^2 = 4 \)に代入して考えると、\( A(0,\sqrt{3}) \)
$B$…
楕円の原点と同じなので、$B(1,0)$
$C$…
$A$の$y$座標と同じはずなので、\( y = \sqrt{3} \)を\( (x-1)^2+y^2 = 4 \)に代入して考えて、\( C(2,\sqrt{3}) \)
すると、$AC$の長さは2とわかり、$AB$と$BC$は円の半径なので、\( AB = BC = 2 \)なので、$△ABC$は正三角形とわかります。
よって、$∠ABC$ = 60°ですから、扇形$ABC$の面積は\( \displaystyle 2・2・π・\frac{60}{360} = \frac{2}{3}π \)
そして、$△ABC$の面積は\( \displaystyle 2・\sqrt{3}・\frac{1}{2} = \sqrt{3} \)
扇形$ABC$から$△ABC$の面積をひけば、求める面積について大きな手がかりが手に入りますね。あとは、$y$軸方向に\( \displaystyle \frac{\sqrt{3}}{2} \)倍すれば楕円に戻りますから、
\( \displaystyle D = \left(\frac{2}{3}π-\sqrt{3}\right)・\frac{\sqrt{3}}{2} \)
\( \displaystyle = \frac{\sqrt{3}}{3}π-\frac{3}{2} \)
答え.
(1)
\( \displaystyle \frac{(x-1)^2}{4}+\frac{y^2}{3} = 1 \)
(2)
\( \displaystyle d = \frac{3}{2} \)
\( \displaystyle D = \frac{\sqrt{3}}{3}π-\frac{3}{2} \)