この問題のポイント
グラフをかくときは、①定義域、②増減・極値、③凹凸・変曲点、④漸近線、⑤x→∞やx→-∞のときの極限、を確認する!
問1 増減や極値を調べるには、$f(x)$を微分すればいいですね。分数関数の形になった式を微分するとこのようになります。
\( \displaystyle \frac{f(x)}{g(x)} \)を微分すると\( \displaystyle \frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2} \)
よって、$f'(x)$は
\( \displaystyle \small{\frac{3x^2\{2(x+4)(2x-1)+2(x+4)^2\} \\ -6x(x+4)^2(2x-1)}{9x^4}} \)
\( \displaystyle \small{= \frac{6x(x+4)\{x(2x-1)+x(x+4)-(x+4)(2x-1)\}}{9x^4}} \)
\( \displaystyle \small{= \frac{6x(x+4)(x-2)^2}{9x^4}} \)
\( \displaystyle \small{= \frac{2(x+4)(x-2)^2}{3x^3}} \)
極値をとるのは\( f'(x) = 0 \)となるときの$x$の値ですから、\( 2(x+4)(x-2)^2 = 0 \)を解いて、\( x = -4,2 \)のときに極値となることがわかります。
そしてグラフの凹凸と変曲点を調べるには、$f''(x)$を求めればいいので、さっき求めた$f'(x)$をもう一度微分します。
\( \displaystyle \small{\frac{3x^3\{2(x-2)^2+4(x+4)(x-2)\} \\ -9x^2・2(x+4)(x-2)^2}{9x^6}} \)
\( \displaystyle \small{= \frac{3x^2(x-2)\{2x(x-2)+4x(x+4)-6(x+4)(x-2)\}}{9x^6}} \)
\( \displaystyle \small{= \frac{3x^2(x-2)・48}{9x^6}} \)
\( \displaystyle \small{= \frac{16(x-2)}{x^4}} \)
変曲点の$x$座標の値は\( f''(x) = 0 \)となるときの$x$の値ですから、\( 16(x-2) = 0 \)を解くことにより、変曲点の$x$座標は2だとわかります。
以上のことをすべて増減表にまとめると、下のとおりになります。
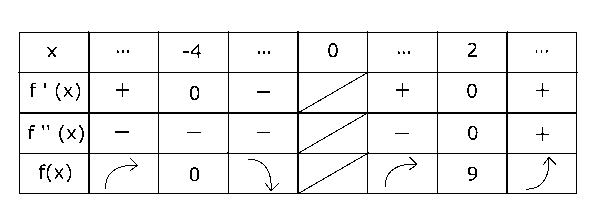
この増減表より、$f(x)$は\( x = -4 \)で極大値0をとり、変曲点は(2,9)をもつことがわかります。
問2 \( \displaystyle g(x) = f(x)-\left(\frac{2}{3}x+5\right) \)より、
$g(x)$
\( \displaystyle = \frac{(x+4)^2(2x-1)}{3x^2}-\left(\frac{2}{3}x+5\right) \)
\( \displaystyle = \frac{24x-16}{3x^2} \)
よって、\( g(x)>0 \)となるためには、\( 24x-16>0 \)とならなければなりませんので、これを解くと、\( \displaystyle x>\frac{2}{3} \)
\(\displaystyle \lim_{x \to \infty} g(x) \)は\(\displaystyle \lim_{x \to \infty} \frac{24x-16}{3x^2} \)であり、分数の部分について、分子・分母両方とも$x$でわると、
\(\displaystyle \lim_{x \to \infty} \frac{24-\frac{16}{x}}{3x} \)
よって、$x$の値を限りなく大きくすると、分母は限りなく大きくなりますが、分子は定数24に限りなく近づくことになります。
\(\displaystyle ∴\lim_{x \to \infty} g(x) = 0 \)
同様に考えると、\(\displaystyle \lim_{x \to -\infty} g(x) = 0 \)
問3 グラフをかくには、このページの上にあった「この問題のポイント」のチェックポイントを確認しなければなりません。まず、定義域についてですが、$f(x)$の分母は0になってはいけないはずですので、\( 3x^2 \neq 0 \)、つまり\( x \neq 0 \)でなければいけません。これは問1の解説にある増減表にもあるとおりです。
そして、増減・極値、凹凸・変曲点についても問1で確認しましたので、次は漸近線を確認しましょう。漸近線は次の性質を使って求めていきましょう。
・漸近線が$y$軸に平行の場合(つまり直線\( x = b \)となる場合)
次のどれかが成立する
\(\displaystyle \lim_{x \to b-0} f(x) = \infty \),\(\displaystyle \lim_{x \to b-0} f(x) = -\infty \)
\(\displaystyle \lim_{x \to b+0} f(x) = \infty \),\(\displaystyle \lim_{x \to b+0} f(x) = -\infty \)
・漸近線が$x$軸に平行の場合(つまり直線\( y = b \)となる場合)
次のどれかが成立する
\(\displaystyle \lim_{x \to \infty} f(x) = b \),\(\displaystyle \lim_{x \to -\infty} f(x) = b \)
・漸近線が直線\( y = ax+b \)となる場合
次のどれかが成立する
\(\displaystyle \lim_{x \to \infty} \{f(x)-(ax+b)\} = 0 \),\(\displaystyle \lim_{x \to -\infty} \{f(x)-(ax+b)\} = 0 \)
これについては、問2にて\(\displaystyle \lim_{x \to \infty} \left\{f(x)-\left(\frac{2}{3}x+5\right)\right\} = 0 \)と求めましたので、漸近線は\(\displaystyle y = \frac{2}{3}x+5 \)とわかります。
最後に、\( x→\infty \)の極値ですが、
\(\displaystyle f(x) = \frac{1}{3}\left(1+\frac{4}{x}\right)^2(2x-1) \)なので、
\(\displaystyle \lim_{x \to 0} f(x) = -\infty \)
そして、漸近線と$f(x)$は共有点をもちます。
\(\displaystyle \frac{(x+4)^2(2x-1)}{3x^2} = \frac{2}{3}x+5 \)には解があるからです。これを解くと、\(\displaystyle x = \frac{2}{3} \)より、共有点は\(\displaystyle \left(\frac{2}{3},\frac{49}{9}\right) \)
以上のことをふまえてグラフをかくと、下のようになります。
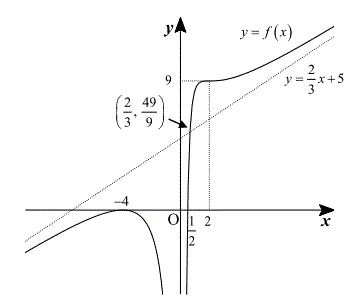
答え.
問1
増減とグラフの凹凸は上の解説の増減表参照
極値は\( x = -4 \)のときの極大値0
変曲点は(2,9)
問2
$x$の範囲は\( \displaystyle x>\frac{2}{3} \)
\(\displaystyle \lim_{x \to \infty} g(x) = 0 \),\(\displaystyle \lim_{x \to -\infty} g(x) = 0 \)
問3
上の解説のグラフ参照