この問題のポイント
sinx/xやx/sinxの極限値は1!
この分数の形が使える形への式変形とはさみうちの原理を使うことを考えよう!
(1)三角関数が混じった式の極限についての問題では、下の定理が使えないかを考えましょう。
\(\displaystyle \lim_{x \to 0} \frac{\sin{x}}{x} = 1 \)
\(\displaystyle \lim_{x \to 0} \frac{x}{\sin{x}} = 1 \)
この形、つまり分母(または分子)の文字とsinの後の文字がそろった形で考えるのが基本になります。この問題の式は、
\( \displaystyle \frac{1}{x}\left(\frac{1}{\sin{x}}-\frac{1}{x}\right) \)
\( \displaystyle = \frac{1}{x\sin{x}}-\frac{1}{x^2} \)
\( \displaystyle = \frac{x-\sin{x}}{x^2\sin{x}} \) …①
とするのが限界なので、そろえることができません。
なので、\( \displaystyle x-\frac{x^3}{6}≦\sin{x}≦x-\frac{x^3}{6}+\frac{x^5}{120} \)を利用することを考えます。
\( \displaystyle -x+\frac{x^3}{6}-\frac{x^5}{120}≦-\sin{x}≦-x+\frac{x^3}{6} \)
\( x≧0 \)より、\( \displaystyle \frac{x^3}{6}-\frac{x^5}{120}≦x-\sin{x}≦\frac{x^3}{6} \)
この辺々に\( \displaystyle \frac{1}{x^2\sin{x}} \)をかけると、
\( \displaystyle \small{\frac{1}{x^2\sin{x}}\left(\frac{x^3}{6}-\frac{x^5}{120}\right)≦\frac{x-\sin{x}}{x^2\sin{x}}≦\frac{1}{x^2\sin{x}}・\frac{x^3}{6}} \)
\( \displaystyle \small{\frac{x}{\sin{x}}\left(\frac{1}{6}-\frac{x^2}{120}\right)≦\frac{x-\sin{x}}{x^2\sin{x}}≦\frac{x}{\sin{x}}・\frac{1}{6}} \)
①の範囲がこれで明らかになりましたが、このような式変形をやったのは、上の赤枠の中にある三角関数の極限の公式を利用するためです。
\(\displaystyle \lim_{x \to 0} \frac{x}{\sin{x}} = 1 \)なんですから、
\(\displaystyle \lim_{x \to +0} \frac{x}{\sin{x}}\left(\frac{1}{6}-\frac{x^2}{120}\right) = \frac{1}{6} \),\(\displaystyle \lim_{x \to +0} \frac{x}{\sin{x}}・\frac{1}{6} = \frac{1}{6} \)
はさみうちの原理より、
\(\displaystyle \lim_{x \to +0} \frac{x-\sin{x}}{x^2\sin{x}} = \frac{1}{6} \)
\(\displaystyle ∴\lim_{x \to +0} \frac{1}{x}\left(\frac{1}{\sin{x}}-\frac{1}{x}\right) = \frac{1}{6} \)
(2)式の形を見ていると(1)となんとなく似ていますよね?これを利用できるように式を変形していきましょう。
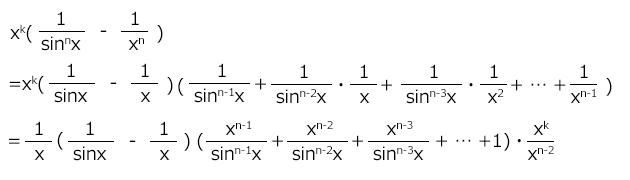
(1)に出てきた\( \displaystyle \frac{1}{x}\left(\frac{1}{\sin{x}}-\frac{1}{x}\right) \)を使った形に変形できました。
(1)より、\(\displaystyle \lim_{x \to +0} \frac{1}{x}\left(\frac{1}{\sin{x}}-\frac{1}{x}\right) = \frac{1}{6} \)で、さらに、
\(\displaystyle \lim_{x \to +0} \left(\frac{x^{n-1}}{\sin^{n-1}{x}}+\frac{x^{n-2}}{\sin^{n-2}{x}}+…+1\right) = n \)です。
よって、問題の条件を満たすためには、
\(\displaystyle \lim_{x \to +0} \frac{x^k}{x^{n-2}} \)
が有限な値に収束して0でないことが条件になります。
そのためには、$x^k$と$x^{n-2}$の次数、つまり、$k$と$n-2$が等しくないといけません。なぜなら、もし\( k>n-2 \)(つまり、$x^●$という形にできる)となると、
\(\displaystyle \lim_{x \to +0} \frac{x^k}{x^{n-2}} = 0 \)となってしまいます。
また、\( k<n-2 \)(つまり、\( \displaystyle \frac{1}{x^●} \)の形にできる)なら、
\(\displaystyle \lim_{x \to +0} \frac{x^k}{x^{n-2}} = \infty \)となってしまいます。
\( k = n-2 \)なら、
\(\displaystyle \lim_{x \to +0} \frac{x^k}{x^{n-2}} = 1 \)
となり、0でない値に収束します。よって、求める条件は\( k = n-2 \)となります。
答え.
(1)\(\displaystyle \frac{1}{6} \)
(2)\( k = n-2 \)