この問題のポイント
楕円の問題で文字や条件が多くなりそうなら媒介変数表示を利用して文字を減らすことも検討しよう!
$P$の座標を$(a,b)$とおくと、これは$C$上の点ですから、\( a^2+4b^2 = 1 \)を満たすことになります。ただ、$l$や$m$の方程式を考えてその後に座標を考えてということを考えると、この状態では直感では計算がしにくいイメージがしますね?
そこで媒介変数表示を利用して扱う文字の数を減らしてみましょう。$P$は楕円上の点で、楕円の方程式は\( x^2+4y^2 = 1 \)ですから、
\( \displaystyle P(\cos{θ},\frac{1}{2}\sin{θ}) \)とおけます。
こうすると、$θ$という1文字だけを考えればよいということになり、少し計算がラクになりそうですね。そうすると、$P$における接線$l$の方程式は、
\( \displaystyle (\cos{θ})x+\left(\frac{1}{2}\sin{θ}\right)・4y = 1 \)
つまり、\( (\cos{θ})x+(2\sin{θ})y = 1 \)です。
次に、$m$の方程式ですが、\( ax+by+c = 0 \)に垂直で点$(x_0,y_0)$を通る直線の方程式は、
\( b(x-x_0)-a(y-y_0) = 0 \)
という公式を使うと、
\( \displaystyle (2\sin{θ})(x-\cos{θ})-(\cos{θ})\left(y-\frac{1}{2}\sin{θ}\right) = 0 \)
整理すると、\( \displaystyle 2\sin{θ}x-\cos{θ}y = \frac{3}{2}\sin{θ}\cos{θ} \)
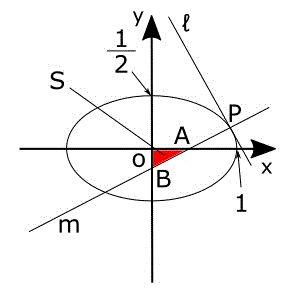
$S$は右の図の$△OAB$(赤色の部分)の面積なんですから、$A$と$B$の座標を考えます。まず、$A$は$m$と$x$軸との交点なので、
\( \displaystyle 2\sin{θ}x = \frac{3}{2}\sin{θ}\cos{θ} \)
\( x>0 \),\( y>0 \)なので\( \sinθ>0 \)ですから、
\( \displaystyle 2x = \frac{3}{2}\cos{θ} \)
\( \displaystyle x = \frac{3}{4}\cos{θ} \)
よって、\( \displaystyle A\left(\frac{3}{4}\cos{θ},0\right) \)です。
$B$は$m$と$y$軸との交点なので、
\( \displaystyle -\cos{θ}y = \frac{3}{2}\sin{θ}\cos{θ} \)
\( x>0 \),\( y>0 \)なので\( \cosθ>0 \)ですから、
\( \displaystyle -y = \frac{3}{2}\sin{θ} \)
\( \displaystyle y = -\frac{3}{2}\sin{θ} \)
よって、\( \displaystyle B\left(0,-\frac{3}{2}\sin{θ}\right) \)です。
よって、$S$の面積は、
\( \displaystyle \frac{1}{2}・\frac{3}{4}\cos{θ}・\frac{3}{2}\sin{θ} \)
\( \displaystyle = \frac{9}{16}\sin{θ}\cos{θ} \)
\( \displaystyle = \frac{9}{16}・\frac{1}{2}\sin{2θ} \)
\( \displaystyle = \frac{9}{32}\sin{2θ} \)
\( x>0 \),\( y>0 \)なので$θ$の範囲は\( \displaystyle 0<θ<\frac{π}{2} \)のため、\( 0<2θ<π \)です。ということは、\( 0<\sin{2θ}≦1 \)ですから、$S$の最大値は\( \displaystyle \frac{9}{32} \)です。
このときの$P$の座標ですが、\( \sin{2θ} = 1 \)のとき、\( \displaystyle 2θ = \frac{π}{2} \)ですから、\( \displaystyle θ = \frac{π}{4} \)です。
\( \displaystyle \cos{\frac{π}{4}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \),\( \displaystyle \frac{1}{2}\sin{\frac{π}{4}} = \frac{1}{2}・\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{4} \)なので、
$P$の座標は\( \displaystyle P\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4}\right) \)です。
(別解)
媒介変数表示を利用せず、$P$の座標を$(a,b)$とおいて解く方法がまったく使えないかというと、そんなことはありません。
$P(a,b)$ただし\( a^2+4b^2 = 1 \)と考えてみます。
$l$は楕円$C$の接線ですから、$m$の方程式は、
\( ax+4by = 1 \)
つまり、\( 4by = -ax+1 \)
\( \displaystyle y = -\frac{a}{4b}x+\frac{1}{4b} \)
2本の直線が垂直に交わるとき、2本の直線の傾きの積は-1になりますから、そのこともあわせて考えると$m$の方程式は、
\( \displaystyle y-b = \frac{4b}{a}(x-a) \)
\( \displaystyle y-b = \frac{4b}{a}x-4b \)
\( \displaystyle y = \frac{4b}{a}x-3b \)
これに\( y = 0 \),\( x = 0 \)を代入して計算すると求まりますが、さっきの図にあった$A$の座標は\( \displaystyle A\left(\frac{3}{4}a,0\right) \)で、$B$の座標は\( (0,-3b) \)です。
よって、\( \displaystyle S = \frac{1}{2}・\frac{3}{4}a・|-3b| \)
\( a>0 \),\( b>0 \)ですから、
\( \displaystyle S = \frac{1}{2}・\frac{3}{4}a・3b = \frac{9}{8}ab \)
ここで、相加平均・相乗平均の関係より、
\( a^2+4b^2≧2\sqrt{a^2・4b^2} \)
\( a^2+4b^2≧2a・2b \)
\( a^2+4b^2≧4ab \)
\( a^2+4b^2 = 1 \)が前提としてあったんですから、
\( 4ab≦1 \)
\( \displaystyle ab≦\frac{1}{4} \)なので
\( \displaystyle S = \frac{9}{8}ab≦\frac{9}{32} \)
これの等号が成立するときは、さっきの相加平均・相乗平均の関係で等号が成立したときになりますから、
\( a^2 = 4b^2 \)が成り立つときですが、\( a^2+4b^2 = 1 \)なのですから、
\( \displaystyle a^2 = 4b^2 = \frac{1}{2} \)が成り立つとき、
つまり、\( \displaystyle a = 2b = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)が成り立つときです。
これより、$S$が最大値\( \displaystyle \frac{9}{32} \)となるとき、$P$の座標は\( \displaystyle P\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4}\right) \)
答え.
$S$の最大値 \( \displaystyle \frac{9}{32} \)
$P$の座標は\( \displaystyle P\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4}\right) \)