この問題のポイント
分母・分子ともに一次式の分数関数は、y = a/(x-p)+qの形になおして考えるのが基本!
\( \displaystyle y = \frac{a}{x} \)という、中学数学で習う反比例の式がありました。これをグラフにあらわしたとして、そのグラフを$x$軸方向に$p$、$y$軸方向に$q$だけ移動させると、
\( \displaystyle y-q = \frac{a}{x-p} \)
\( \displaystyle y = \frac{a}{x-p}+q \)
となります。これこそが分数関数の基本形であり、これになおしてから考えるほうがわかりやすくなります。
問題文の式も基本形とだいぶ違う形になっているのでこのままだと考えにくいですから、上の基本形になるように式を変形させましょう。
\begin{eqnarray} &&y = \frac{ax-1}{a-x}\\ &&= \frac{-ax+1}{x-a}\\ &&= \frac{-a(x-a)-a^2+1}{x-a}\\ &&= \frac{-a^2+1}{x-a}-a\\ \end{eqnarray}
基本形に変形できましたが、$a$は正の実数ということしかわからず、値を特定できませんから、$-a^2+1$が正の数になるのか負の数になるのかはわかりません。よって、それに応じてグラフの形が違うようになりますから、場合分けして考えましょう。
[1]\( -a^2+1>0 \)
つまり\( a^2<1 \)
\( 0<a<1 \)のとき
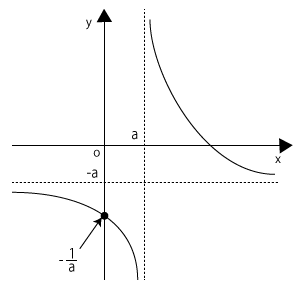
問題文にあった分数関数をグラフにすると右の図のようになります。\( x≧0 \)のときの$y$の範囲を調べればいいので、$y$軸より右側部分だけを考えればいいことになります。
\( \displaystyle y = -\frac{1}{a} \)から下がっている曲線と、漸近線\( y = -a \)より上側に描かれた曲線の2本がありますから、$y$のとりうる値の範囲は
\( \displaystyle y≦-\frac{1}{a} \),\( -a<y \)です。
[2]\( -a^2+1 = 0 \)
つまり\( a^2 = 1 \)
\( a>0 \)より\( a = 1 \)のとき
\( \displaystyle y = \frac{-a^2+1}{x-a}-a \)は\( y = -a \)となります。これは\( a = 1 \)のときの話なので、\( y = -1 \)となり、グラフにすると、$x$軸と平行な横向きの直線がひかれることになりますから、このときの$y$のとりうる値は\( y = -1 \)しかありません。
[3]\( -a^2+1<0 \)
つまり\( a^2>1 \)
\( a>0 \)より\( 1<a \)のとき
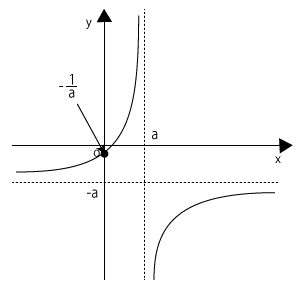
問題文にあった分数関数をグラフにすると、この場合は右の図のようになります。[1]のときと同じように、$y$軸より右側部分だけを考えると、\( \displaystyle y = -\frac{1}{a} \)から上がっている曲線と、漸近線\( y = -a \)より下側に描かれた曲線の2本がありますから、$y$のとりうる値の範囲は
\( y<-a \),\( \displaystyle -\frac{1}{a}≦y \)です。
答え.
\( 0<a<1 \)のとき、\( \displaystyle y≦-\frac{1}{a} \),\( -a<y \)
\( a = 1 \)のとき、\( y = -1 \)
\( 1<a \)のとき、\( y<-a \),\( \displaystyle -\frac{1}{a}≦y \)