問題ページにもどる

この問題のポイント

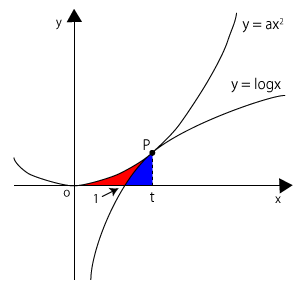
（１）\( f(x) = \log x \)，\( g(x) = ax^2 \)とします。まず、$P$の座標を求めることを考えてみましょう。$f(x)$と$g(x)$は点$P$で接しているんですから、右の図のような関係になるはずですね。

このとき、グラフより、点$P$の$x$座標を$t$とすると、\( f(t) = g(t) \)といえます。ちなみに、グラフより、\( t＞0 \)です。
よって、\( \log t = at^2 \) …①

また、単に交わっているのではなく、接しているんですから、点$P$において2曲線の接線も共通となります。ということは、接線の傾きは等しいわけなんですから、$f'(t)$と$g'(t)$も等しいですね？接しているときは、このように微分した値も等しくなることのチェックを忘れずにしましょう！

$f(x)$と$g(x)$を微分すると、それぞれこのようになります。
\( \displaystyle f'(x) = \frac{1}{x} \)，\( g'(x) = 2ax \)
\( f'(t) = g'(t) \)より、\( \displaystyle \frac{1}{t} = 2at \) …②

ここで②より、\( 2at^2 = 1 \)なので、
\( \displaystyle at^2 = \frac{1}{2} \) …③

これを①に代入すると、
\( \displaystyle \log t = \frac{1}{2} \)
よって、\( t = \sqrt{e} \)となります。これは、さっき書いた\( t＞0 \)も満たしていますね。

そして$a$の値ですが、これは\( t = \sqrt{e} \)を③に代入すると求まります。
\( \displaystyle ea = \frac{1}{2} \)ですから、\( \displaystyle a = \frac{1}{2e} \)ですね。

（２）$x$軸のまわりに回転させてできる立体の体積は、下の公式で求めることができます。

\( y = f(x) \)，\( x = a \)，\( x = b \)，$x$軸で囲まれた領域を$x$軸のまわりに回転させてできた立体の体積は、

\( \displaystyle \int_a^b π\{f(x)\}^2dx \)

要するに、回転体の切り口は円であり、その半径は$f(x)$の値になるので、断面積は\( π\{f(x)\}^2 \)となります。それを\( a≦x≦b \)で積分しているというわけです。

さて、回転軸のまわりに回転させなければならないのは、さっきの図の赤色の部分ということになります。この部分は、一部が$x$軸ではなく、\( y = \log x \)の部分に囲まれているんで、さっきの公式を単にあてはめて解けるというわけではありません。

たとえば、\( t = \sqrt{e} \)なんですから、さっきの公式を使って、\( 0≦x≦\sqrt{e} \)の範囲でこのように考えたとしましょう。

\( \displaystyle \int_0^{\sqrt{e}} π\left(\frac{1}{2e}x^2\right)^2dx \)

この式では、（１）で示した図でいうと、赤色の部分と青色の部分を合わせたものの回転体の体積が求まってしまいます。よって、ここから青色の部分をひきましょう。
青色の部分は、ちょうど\( 1≦x≦\sqrt{e} \)の範囲で\( y = \log x \)を回転させた部分になりますから、

\begin{eqnarray} &&\int_0^{\sqrt{e}} π\left(\frac{1}{2e}x^2\right)^2dx\\ &&~~~~-\int_1^{\sqrt{e}} π(\log x)^2dx\\ &&= π\left[\frac{1}{4e^2}×\frac{x^5}{5}\right]_0^{\sqrt{e}}\\ &&~~~~-π\int_1^{\sqrt{e}} (x)'(\log x)^2dx\\ &&= π×\frac{e^2\sqrt{e}}{20e^2}\\ &&~~~~-π\left[x(\log x)^2\right]_1^{\sqrt{e}}+π\int_1^{\sqrt{e}} x・2(\log x)×\frac{1}{x}dx\\ &&= \frac{\sqrt{e}}{20}π\\ &&~~~~-\sqrt{e}×\left(\frac{1}{2}\right)^2π+2π\int_1^{\sqrt{e}} (x)'\log xdx\\ &&= \frac{\sqrt{e}}{20}π\\ &&~~~~-\frac{\sqrt{e}}{4}π+2π\left[x\log x\right]_1^{\sqrt{e}}-2π\int_1^{\sqrt{e}} 1dx\\ &&= \frac{-4\sqrt{e}}{20}π+2π\sqrt{e}×\frac{1}{2}-2π・\left[x\right]_1^{\sqrt{e}}\\ &&= -\frac{\sqrt{e}}{5}π+\sqrt{e}π-2\sqrt{e}π+2π\\ \end{eqnarray}

\begin{eqnarray} &&\small{\int_0^{\sqrt{e}} π\left(\frac{1}{2e}x^2\right)^2dx}\\ &&\small{~~~~-\int_1^{\sqrt{e}} π(\log x)^2dx}\\ &&\small{= π\left[\frac{1}{4e^2}×\frac{x^5}{5}\right]_0^{\sqrt{e}}}\\ &&\small{~~~~-π\int_1^{\sqrt{e}} (x)'(\log x)^2dx}\\ &&\small{= π×\frac{e^2\sqrt{e}}{20e^2}}\\ &&\small{~~~~-π\left[x(\log x)^2\right]_1^{\sqrt{e}}+π\int_1^{\sqrt{e}} x・2(\log x)×\frac{1}{x}dx}\\ &&\small{= \frac{\sqrt{e}}{20}π}\\ &&\small{~~~~-\sqrt{e}×\left(\frac{1}{2}\right)^2π+2π\int_1^{\sqrt{e}} (x)'\log xdx}\\ &&\small{= \frac{\sqrt{e}}{20}π}\\ &&\small{~~~~-\frac{\sqrt{e}}{4}π+2π\left[x\log x\right]_1^{\sqrt{e}}-2π\int_1^{\sqrt{e}} 1dx}\\ &&\small{= \frac{-4\sqrt{e}}{20}π+2π\sqrt{e}×\frac{1}{2}-2π・\left[x\right]_1^{\sqrt{e}}}\\ &&\small{= -\frac{\sqrt{e}}{5}π+\sqrt{e}π-2\sqrt{e}π+2π}\\ \end{eqnarray}

このように計算できますから、結果、\( \displaystyle \left(2-\frac{6}{5}\sqrt{e}\right)π \)となります。

答え．
（１）
\( \displaystyle P\left(\sqrt{e},\frac{1}{2}\right) \)
\( \displaystyle a = \frac{1}{2e} \)
（２）
\( \displaystyle \left(2-\frac{6}{5}\sqrt{e}\right)π \)