極方程式と円－中学・高校の問題演習ができるホームページ

この問題のポイント

極方程式をxy方程式に書き換えて考えよう！
r² = x²+y²
x = rcosθ
y = rsinθを利用しよう！

（１）原点から点$A$までの距離（$r$）と、点$A$と原点と$x$軸を結ぶ線とのなす角（$θ$）で表した方程式を極方程式といいます。

この極方程式の表し方では、「これは円の方程式です」と言われても、中心の座標がどこかなどということがすぐにわからないようになっています。それがすぐにわかるようにするには、$xy$方程式のほうが便利ですね？

というわけで、極方程式を$xy$方程式に書き換えます。その書き換えで使えるのが、上に挙げた3つの式です。

まず、問題に出てた極方程式には、$r^2$も$ \cosθ $もありません（$r$とか$ \cos{(a-θ)} $ならありますが）。なので、その形を「作り」ます。両辺に$r$をかけて、さらに加法定理を使って変形すると、

$ r^2 = 2ar\cos{(a-θ)} $
$ r^2 = 2ar(\cos{a}\cos{θ}+\sin{a}\sin{θ}) $
$ r^2 = r\cos{θ}・2a\cos{a}+r\sin{θ}・2a\sin{a} $

これで、$r^2$も$ r\cosθ $，$ r\sinθ $も出てきましたから、このようになります。

$ x^2+y^2 = 2ax\cos{a}+2ay\sin{a} $
$ x^2-2ax\cos{a}+y^2-2ay\sin{a} = 0 $

ここで、円の方程式の形にするために平方完成をすると、

\begin{eqnarray} &&(x^2-2ax\cos{a}+a^2\cos^2{a})-a^2\cos^2{a}\\ &&~~~~+(y^2-2ay\sin{a}+a^2\sin^2{a})-a^2\sin^2{a} = 0\\ &&(x-a\cos{a})^2+(y-a\sin{a})^2\\ &&~~~~= a^2\cos^2{a}+a^2\sin^2{a}\\ &&(x-a\cos{a})^2+(y-a\sin{a})^2\\ &&~~~~= a^2(\cos^2{a}+\sin^2{a})\\ \end{eqnarray}

$ \cos^2{θ}+\sin^2{θ} = 1 $ですから、
$ (x-a\cos{a})^2+(y-a\sin{a})^2 = a^2 $

これで、円になることが示されました。そして、この式より、中心は$ (a\cos{a},a\sin{a}) $であり、半径は$a$だということもわかります。

解答のチェックポイント

極方程式から$xy$方程式に書き換えて考えているか
$ \cos{(a-θ)} $を加法定理を使って変形したか
平方完成をして円の方程式を完成させることができたか

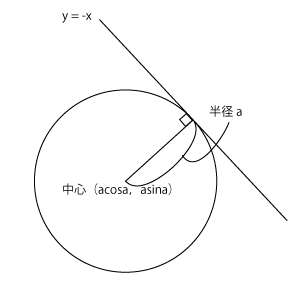
（２）円が直線$ y = -x $と接しているということは、右図のような関係になっているということです。この図からわかるとおり、中心である点$ (a\cos{a},a\sin{a}) $と直線$ y = -x $つまり$ x+y = 0 $の距離が、ちょうど半径$a$と等しくなっている関係になっています。

ということで、点と直線の距離の公式を使うと、このような式ができあがります。

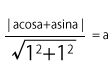
分母が$ \sqrt{2} $となりますから、
$ |a\cos{a}+a\sin{a}| = \sqrt{2}a $

絶対値が$ \sqrt{2}a $ということですから、
$ a\cos{a}+a\sin{a} = ±\sqrt{2}a $
$ a(\cos{a}+\sin{a}) = ±\sqrt{2}a $
$ \cos{a}+\sin{a} = ±\sqrt{2} $

三角関数の合成を使って変形すると、
$ \displaystyle \sqrt{2}\sin(a+\frac{π}{4}) = ±\sqrt{2} $
$ \displaystyle \sin(a+\frac{π}{4}) = ±1 $
$ \displaystyle a+\frac{π}{4} = \frac{π}{2}+nπ $（$n$は整数）

よって、$ \displaystyle a = \frac{π}{4}+nπ $
ただし、$a$は正の実数ですから、$n$は0以上の整数です。

答え．
（１）
（円になることの証明は上の解説参照）
中心　$ (a\cos{a},a\sin{a}) $　　　半径　$a$
（２）
$ \displaystyle a = \frac{π}{4}+nπ $（$n$は0以上の整数）