この問題のポイント
逆数との和の形があれば相加平均・相乗平均が使える!
x+yやxyのどちらかが具体的な数ならば、相加平均・相乗平均を使ってもう片方の最大値や最小値も求まる!
(1)与えられた式を展開すると、
\( \displaystyle \left(x+\frac{1}{y}\right)\left(y+\frac{4}{x}\right) \)
\( \displaystyle = xy+4+1+\frac{4}{xy} \)
\( \displaystyle = xy+\frac{4}{xy}+5 \) …①
$xy$と\( \displaystyle \frac{4}{xy} \)という部分がありますが、このように、ある数とその数が分母にある分数が同時にある式について考えるときは相加平均・相乗平均の関係が使えるのではないかと考えてみましょう。
相加平均・相乗平均の関係とは次のようなものです。
相加平均・相乗平均の関係
$a>0$,$b>0$のとき
\( \displaystyle \frac{a+b}{2}≧\sqrt{ab} \)
つまり、\( a+b≧2\sqrt{ab} \)
等号が成立するのは、$a = b$のときである
問題文より、\( x>0 \),\( y>0 \)とありましたから、相加平均・相乗平均の関係を利用することができます。すなわち、①の式にあった\( \displaystyle xy+\frac{4}{xy} \)について、
\( \displaystyle xy+\frac{4}{xy}≧2\sqrt{xy・\frac{4}{xy}} \)が成り立ちます。
よって、\( \displaystyle xy+\frac{4}{xy}≧2\sqrt{4} \)
\( \displaystyle xy+\frac{4}{xy}≧2・2 \)
\( \displaystyle xy+\frac{4}{xy}≧4 \)
この式の両辺に5を加えると、\( \displaystyle xy+\frac{4}{xy}+5≧4+5 \)
\( \displaystyle xy+\frac{4}{xy}+5≧9 \) …A
よって、①の式の最小値は9と考えることができます。
ただし、これで終わりにしてはいけません。相加平均・相乗平均の関係を利用した場合は、必ず等号が成立するのはどんなときかを確認する必要があります。さっきのAの式も、本当の最小値は10だとしても、一応成立します。本当に最小値として9をとるときがあるのかを示さないといけないわけです。
Aの式で等号が成立するときは、
\( \displaystyle xy = \frac{4}{xy} \)のとき、つまり
\( x^2y^2 = 4 \)
\( xy = 2 \)のときで、このときに最小値9をとります。
(2)\( \displaystyle 4x^2+\frac{1}{(x+1)(x-1)} \)の分母を展開すると、
\( \displaystyle 4x^2+\frac{1}{x^2-1} \)となり、分数の分子と分母両方を4倍すると、
\( \displaystyle 4x^2+\frac{4}{4x^2-4} \) …②
なぜ分子と分母両方を4倍したかというと、このようにすると、$4x^2$が分母にも出てくるので、相加平均・相乗平均の関係が利用できそうになるからです。ちょうど、\( x>1 \)と問題文にもありましたから、$4x^2$も\( \displaystyle \frac{4}{4x^2-4} \)も0より大きいですから、相加平均・相乗平均の関係を問題なく使えそうです。
ところが、実際に使ってみると、
\( \displaystyle 4x^2+\frac{4}{4x^2-4}≧2\sqrt{4x^2・\frac{4}{4x^2-4}} \)
となり、さっきの(1)のようにルートの中が約分できないので、これ以上進めることができません。分数の分母にあるものとまったく同じものがないといけないというわけですね。
そういうときは、分数の分母と同じものができるように式を変形していきましょう。もちろん、勝手に足したり引いたりしたら式が変わってしまいます。たとえば、②の場合なら、このように変えてみましょう。
\( \displaystyle 4x^2-4+4+\frac{4}{4x^2-4} \)
\( \displaystyle = 4x^2-4+\frac{4}{4x^2-4}+4 \)
このように、足したら同じ値を引くということを忘れずに式を変形すればいいわけです。すると、相加平均・相乗平均の関係より、
\( \displaystyle 4x^2-4+\frac{4}{4x^2-4}+4≧2\sqrt{(4x^2-4)・\frac{4}{4x^2-4}}+4 \)
\( \displaystyle 4x^2-4+\frac{4}{4x^2-4}+4≧2\sqrt{4}+4 \)
\( \displaystyle 4x^2-4+\frac{4}{4x^2-4}+4≧2・2+4 \)
\( \displaystyle 4x^2-4+\frac{4}{4x^2-4}+4≧8 \)
\( \displaystyle 4x^2+\frac{4}{4x^2-4}≧8 \)
よって、②の最小値、つまり\( \displaystyle 4x^2+\frac{1}{(x+1)(x-1)} \)の最小値は8と考えられます。次に、等号が成立するときを確認します。
相加平均・相乗平均の関係にあてはめたのは$4x^2-4$と\( \displaystyle \frac{4}{4x^2-4} \)でしたから、
\( \displaystyle 4x^2-4 = \frac{4}{4x^2-4} \)のときに等号が成立します。
この方程式を解くと、
\( (4x^2-4)^2 = 4 \)
\( 4x^2-4 = ±2 \)
問題文より、\( x>1 \)ですから\( 4x^2-4>0 \)なので、\( 4x^2-4 = 2 \)
\( 4x^2 = 6 \)
\( \displaystyle x^2 = \frac{3}{2} \)
\( x>1 \)なので、\( \displaystyle x = \sqrt{\frac{3}{2}} = \frac{\sqrt{3}}{\sqrt{2}} = \frac{\sqrt{6}}{2} \)
このときに等号が成立し、最小値8をとるわけですね。
(3)〈指針〉
証明する不等式の左辺を\( x+y = 1 \)ということもあわせて展開すると、今回はある数とその数が分母にある分数が同時にある式になりません。そのかわり、\( \displaystyle \frac{2}{xy} \)という$xy$が分母となった分数が式の中にあらわれます。
この問題では、$x+y$の値がわかっていますが、相加平均・相乗平均の関係を示す不等式に出ている$x+y$と$xy$について、このどちらか片方の値がわかっている場合も、相加平均・相乗平均の関係が問題を解くカギとなることが多いです。
つまり、相加平均・相乗平均の関係を使って、\( \displaystyle \frac{2}{xy} \)がどういう範囲をとるかを示し、それを利用して証明したい不等式の成立を示すという方法をとるわけです。もちろん、それを使うときは、前提となる\( x>0 \),\( y>0 \)ということの確認と、問題でも求められていますが、等号が成立するときの確認は必ずしましょう。
〈証明〉
\( \displaystyle \left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)≧9 \)の左辺を
展開すると、
\( \displaystyle 1+\frac{1}{y}+\frac{1}{x}+\frac{1}{xy}≧9 \)
\( \displaystyle 1+\frac{x+y}{xy}+\frac{1}{xy}≧9 \)
\( x+y = 1 \)より、\( \displaystyle 1+\frac{1}{xy}+\frac{1}{xy}≧9 \)
\( \displaystyle 1+\frac{2}{xy}≧9 \)
\( \displaystyle \frac{2}{xy}≧8 \) …③
ここで、\( x>0 \),\( y>0 \)なので、相加平均・相乗平均の関係より、
\( x+y≧2\sqrt{xy} \)が成り立ち、\( x+y = 1 \)なので、
\( 1≧2\sqrt{xy} \)
\( \displaystyle \sqrt{xy}≦\frac{1}{2} \)
これより、\( \displaystyle xy≦\frac{1}{4} \)なので、
\( \displaystyle \frac{1}{xy}≧4 \)
\( \displaystyle \frac{2}{xy}≧8 \)
③が示されたので、\( \displaystyle \left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)≧9 \)が成り立つ。
等号が成立するときは、\( x = y \)が成り立つとき、すなわち\( x+y = 1 \)なので\( \displaystyle x = y = \frac{1}{2} \)のときである。
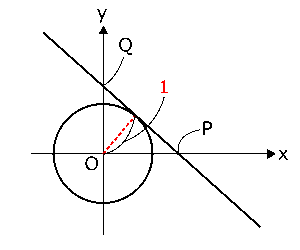
(4)直線$PQ$は円と接しているんですから、右の図のような位置関係になるはずです。図からわかるとおり、円の中心である原点\( (0,0) \)と直線$PQ$との距離は円の半径である1と等しいことになります。図のとおり、直線$PQ$は右下がりの直線なので、$m>0$,$n>0$として直線$PQ$の方程式を\( y = -mx+n \)、つまり\( mx+y-n = 0 \)とおいてみましょう。
点と直線の距離の公式を使って、
\( \displaystyle \frac{|m・0+0-n|}{\sqrt{m^2+1^2}} = 1 \)
\( \displaystyle \frac{|-n|}{\sqrt{m^2+1}} = 1 \)
$n>0$なので\( \displaystyle \frac{n}{\sqrt{m^2+1}} = 1 \)
\( n = \sqrt{m^2+1} \)
\( n^2 = m^2+1 \) …④
直線$PQ$の方程式を\( y = -mx+n \)としたので、$P$の座標は\( \displaystyle \left(\frac{n}{m},0\right) \),$Q$の座標は\( (0,n) \)となります。よって、
\( aOP^2+bOQ^2 \)
\( \displaystyle = a・\left(\frac{n}{m}\right)^2+bn^2 \)
\( \displaystyle = a・\frac{n^2}{m^2}+bn^2 \)
④より、\( \displaystyle a・\frac{m^2+1}{m^2}+b(m^2+1) \)
\( \displaystyle = a\left(1+\frac{1}{m^2}\right)+b(m^2+1) \)
\( \displaystyle = a+\frac{a}{m^2}+bm^2+b \)
\( \displaystyle = \frac{a}{m^2}+bm^2+a+b \) …⑤
ここで、\( \displaystyle \frac{a}{m^2}+bm^2 \)の部分について、ある数とその数が分母にある分数が同時にあるような形になっていて、$m>0$でもありますから、相加平均・相乗平均の関係を使ってみると、
\( \displaystyle \frac{a}{m^2}+bm^2≧2\sqrt{\frac{a}{m^2}・bm^2} \)
\( \displaystyle \frac{a}{m^2}+bm^2≧2\sqrt{ab} \)
これの両辺に$a+b$を加えると、$a$,$b$は正の定数なので不等号の向きは変わりませんから、\( \displaystyle \frac{a}{m^2}+bm^2+a+b≧2\sqrt{ab}+a+b \)
\( \displaystyle \frac{a}{m^2}+bm^2+a+b≧(\sqrt{a}+\sqrt{b})^2 \)
⑤の式と同じ形になりましたから、\( aOP^2+bOQ^2 \)の最小値は\( (\sqrt{a}+\sqrt{b})^2 \)です。
等号が成立するときは、\( \displaystyle \frac{a}{m^2} = bm^2 \)
\( bm^4 = a \)
\( \displaystyle m^4 = \frac{a}{b} \)
\( \displaystyle m = \sqrt[4] {\frac{a}{b}} \)のときです。
答え.
(1)9
(2)最小値…8 そのときの$x$の値…\( \displaystyle \frac{\sqrt{6}}{2} \)
(3)(上の〈証明〉参照)
(4)\( (\sqrt{a}+\sqrt{b})^2 \)