この問題のポイント
f(x) = tの解は、y = f(x)のグラフとy = tのグラフの交点のx座標と同じ!
それぞれの解の範囲もグラフから考えることができる!
(1)\( f(x) = (x-a)(x-b)(x-c) \)を展開すると、
\( f(x) = x^3-(a+b+c)x^2+(ab+bc+ca)x-abc \)…①
\( a+b+c = 3 \),$abc = t$なので、①の式は\( f(x) = x^3-3x^2+(ab+bc+ca)x-t \)とおけます。あとは$ab+bc+ca$の値が求まれば解けそうですから、それを考えます。
\( (a+b+c)^2 = a^2+b^2+c^2+2ab+2bc+2ca \)なので、
\( (a+b+c)^2 = a^2+b^2+c^2+2(ab+bc+ca) \)より、
\( 3^2 = 27+2(ab+bc+ca) \)
\( 2(ab+bc+ca) = -18 \)
\( ab+bc+ca = -9 \)
よって、①の式は\( f(x) = x^3-3x^2-9x-t \)とおけます。
(2)\( f(x) = (x-a)(x-b)(x-c) \)なので、\( f(x) = 0 \)という方程式があれば、$a$,$b$,$c$はこの方程式の解であるということができます。
ならば、\( f(x) = 0 \)は3つの実数解を持つことになるので、この方程式が3つの実数解を持つのはどんなときかを考えます。
さっきの(1)より、$f(x)$は\( x^3-3x^2-9x-t \)ともおけるので、
\( x^3-3x^2-9x-t = 0 \)
つまり、\( x^3-3x^2-9x = t \)
が3つの実数解を持つのはどんなときかを考えましょう。
\( x^3-3x^2-9x = t \)というのは、\( y = x^3-3x^2-9x \)と\( y = t \)を連立方程式にして解くのと同じことです。中学数学で、連立方程式の解は2つのグラフの交点の座標と同じということを勉強しましたが、それと同じように考えると、\( y = x^3-3x^2-9x \)と\( y = t \)の交点を考えればいいということになります。
そこで、\( y = x^3-3x^2-9x \)がどんなグラフになるかを考えると、これを微分して、
\( y' = 3x^2-6x-9 \)
\( = 3(x^2-2x-3) \)
\( = 3(x-3)(x+1) \)
これより、\( y' = 0 \)となるのは$x$が-1と3のときなので、増減表はこのようになります。
| $x$ | … | -1 | … | 3 | … |
| $y'$ | + | 0 | - | 0 | + |
| $y$ | ↗ | 5 | ↘ | -27 | ↗ |
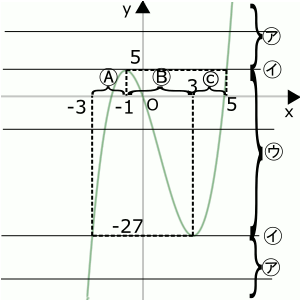
よって、\( y = x^3-3x^2-9x \)のグラフは右の図の緑色の曲線のようになります。\( y = t \)のグラフは$x$軸と平行な直線となります。この2つのグラフの交点が3つあるときを考えると、
\( y = t \)のグラフが㋐の範囲内にあるとき
…交点は1つ
\( y = t \)のグラフが㋑の位置にあるとき
…交点は2つ
\( y = t \)のグラフが㋒の範囲内にあるとき
…交点は3つ
ただし、3つの解である$a$,$b$,$c$は\( a≦b≦c \)という関係なので重解がある可能性もあるので、\( y = t \)のグラフがある範囲は㋑か㋒ということになりますので、求める範囲は\( -27≦t≦5 \)です。
(3)\( f(x) = 0 \)は、さっきの(2)で考えたとおり、\( x^3-3x^2-9x = t \)と置き換えることができますから、さっきの2つのグラフの交点を考えればいいですね?その交点の座標を考えながら、\( a+b+c = 3 \),\( a^2+b^2+c^2 = 27 \)を満たす整数を考えることとなります。
ただし、条件がこれだけでは考えることができません。条件を満たす整数を考えるときは、整数の範囲をしぼることが一つの手です。この問題でも、その範囲をしぼることを考えてみましょう。
方程式の解、つまりグラフの交点の$x$座標を示す$a$,$b$,$c$は\( a≦b≦c \)という関係です。ということは、3つある交点のうち、$a$は一番左,$b$は中央,$c$は一番右にあるんですから、$a$はⒶ,$b$はⒷ,$c$はⒸのそれぞれの範囲内に必ずあります。
そこで、$x = -1$以外に\( x^3-3x^2-9x = 5 \)となる点の$x$座標を考えると、$x = -1$を解に持つならば$x+1$で因数分解できるはずなので、
\( (x+1)(x^2-4x-5) = 0 \)
\( (x+1)(x-5)(x+1) = 0 \)
\( (x+1)^2(x-5) = 0 \)なので$x = 5$
$x = 3$以外に\( x^3-3x^2-9x = -27 \)となる点の$x$座標を考えると、$x = 3$を解に持つならば$x-3$で因数分解できるはずなので、
\( (x-3)(x^2-9) = 0 \)
\( (x-3)(x+3)(x-3) = 0 \)
\( (x-3)^2(x+3) = 0 \)なので$x = -3$
これより、\( -3≦a≦-1 \),\( -1≦b≦3 \),\( 3≦c≦5 \)とわかりました。$a$,$b$,$c$が整数であるなら、$a$は-3か-2か-1のいずれかということになります。この3つそれぞれについて、$b$や$c$はどうなのかを考えていきます。
[1]$a = -3$の場合
\( a+b+c = 3 \)なので、\( b+c = 6 \)
\( a^2+b^2+c^2 = 27 \)なので、\( (-3)^2+b^2+c^2 = 27 \)より、\( b^2+c^2 = 18 \)
\( b^2+c^2 = (b+c)^2-2bc \)より、\( 18 = 6^2-2bc \)
\( 2bc = 18 \)
\( bc = 9 \)
解と係数の関係より、$b$,$c$は二次方程式\( x^2-6x+9 = 0 \)の解だといえます。
この方程式を解くと、\( (x-3)^2 = 0 \)より、$x = 3$
つまり、$b$,$c$は重解ということで両方とも3という値であるということです。
これは\( -1≦b≦3 \),\( 3≦c≦5 \)という範囲にもきちんと合致しています。
[2]$a = -2$の場合
\( a+b+c = 3 \)なので、\( b+c = 5 \)
\( a^2+b^2+c^2 = 27 \)なので、\( (-2)^2+b^2+c^2 = 27 \)より、\( b^2+c^2 = 23 \)
さっきの[1]と同様にして、
\( b^2+c^2 = (b+c)^2-2bc \)
\( 23 = 5^2-2bc \)
\( 2bc = 2 \)
\( bc = 1 \)
解と係数の関係より、$b$,$c$は二次方程式\( x^2-x+5 = 0 \)の解だといえます。
ところが、この方程式の判別式\( D = (-1)^2-4・1・5 = -19 \)より、方程式の解はないことになります。
つまり、$b$,$c$の値がないということになるんで、$a = -2$の場合は成立しないこととなります。
[3]$a = -1$の場合
\( a+b+c = 3 \)なので、\( b+c = 4 \)
\( a^2+b^2+c^2 = 27 \)なので、\( (-1)^2+b^2+c^2 = 27 \)より、\( b^2+c^2 = 26 \)
さっきの[1]や[2]と同様にして、
\( b^2+c^2 = (b+c)^2-2bc \)
\( 26 = 4^2-2bc \)
\( 2bc = -10 \)
\( bc = -5 \)
解と係数の関係より、$b$,$c$は二次方程式\( x^2-4x-5 = 0 \)の解だといえます。
この方程式を解くと、\( (x-5)(x+1) = 0 \)より、$x = 5,-1$
\( -1≦b≦3 \),\( 3≦c≦5 \)という範囲とてらしあわせて考えると、$b = -1$,$c = 5$
よって、[1]~[3]より、$a$,$b$,$c$の値は\( (a,b,c) \) = (-3,3,3),(-1,-1,5)
答え.
(1)\( f(x) = x^3-3x^2-9x-t \)
(2)\( -27≦t≦5 \)
(3)\( (a,b,c) \) = (-3,3,3),(-1,-1,5)