この問題のポイント
円の接線の方程式を考えるときは接線の公式だけでなく「接線と中心の距離は円の半径に等しい」という視点も持つ!
(1)②の方程式を\( (x-a)^2+(y-b)^2 = ● \)の形にしていくと、
\( x^2-2kx+y^2+3k = 0 \)
\( x^2-2kx+k^2-k^2+y^2+3k = 0 \)
\( (x-k)^2+y^2-k^2+3k = 0 \)
\( (x-k)^2+y^2 = k^2-3k \)
\( (x-a)^2+(y-b)^2 = ● \)で表された円の方程式について、●の部分は半径の2乗でした。②が円となるということは、この半径の2乗がちゃんと0より大きい数になるということですから、
\( k^2-3k>0 \)
これを解くと、
\( k(k-3)>0 \)
\( k<0,3<k \)
(2)①は中心が\( (0,0) \)で半径が1の円です。そして、さっきの(1)で②の方程式を変形したことで、②は中心が\( (k,0) \)で半径が\( \sqrt{k^2-3k} \)の円とわかりました。
2つの円が共有点をもつとき、その2つの円の中心間の距離は、円どうしの半径の差より大きく、円どうしの半径の和より小さいということになります。①と②の中心間の距離は$|k|$ですから、
\( |\sqrt{k^2-3k}-1|<k<\sqrt{k^2-3k}+1 \)が成り立ちます。
それぞれを2乗して\( (\sqrt{k^2-3k}-1)^2<k^2<(\sqrt{k^2-3k}+1)^2 \)
\( (\sqrt{k^2-3k}-1)^2<k^2 \)より、\( k^2-3k+1-2\sqrt{k^2-3k}<k^2 \)
\( -3k+1<2\sqrt{k^2-3k} \)…A
\( k^2<(\sqrt{k^2-3k}+1)^2 \)より、\( k^2<k^2-3k+1+2\sqrt{k^2-3k} \)
\( 3k-1<2\sqrt{k^2-3k} \)…B
A,Bより、\( |3k-1|<2\sqrt{k^2-3k} \)と同じことになっていることがわかります。
この式の両辺を2乗して、
\( (3k-1)^2<4(k^2-3k) \)
\( 9k^2-6k+1<4k^2-12k \)
\( 5k^2+6k+1<0 \)
\( (k+1)(5k+1)<0 \)
これを解くと、\( \displaystyle -1<k<-\frac{1}{5} \)
ただし、②が円の方程式となっている、つまりさっきの(1)で求めた範囲を満たしている必要があります。\( \displaystyle -1<k<-\frac{1}{5} \)はその範囲を満たしているので、そのまま答えとしてかまわないことになります。
(3)$k = 4$なので、円②は中心が\( (4,0) \)で半径が\( \sqrt{4^2-3・4} = 2 \)の円となります。さて、この問題では接線を求めることとなるのですが、円の接線の方程式はこのように表すことができましたね?
円の接線の方程式
円\( x^2+y^2 = r^2 \)の円周上の点\( (p,q) \)に接する接線の方程式は
\( px+qy = r^2 \)
円\( (x-a)^2+(y-b)^2 = r^2 \)の円周上の点\( (p,q) \)に接する接線の方程式は
\( (p-a)(x-a)+(q-b)(y-b) = r^2 \)
よって、円①に点\( (p,q) \)で接すると考えると、接線の方程式は\( px+qy = 1 \)…Cとおけます。そして、点\( (p,q) \)は円①の点ですから、\( p^2+q^2 = 1 \)…Dでもあります。
そして、Cの方程式で表された接線は円②にも接します。直線が円に接するということは、直線と円の中心との距離がそのまま円の半径になっているということです。$k = 4$なので、円②の中心は\( (4,0) \)で半径は2ですから、点と直線の距離の公式を利用して、
\( \displaystyle \frac{|4p+0・y-1|}{\sqrt{p^2+q^2}} = 2 \)
\( \displaystyle \frac{|4p-1|}{\sqrt{p^2+q^2}} = 2 \)
Dより、\( p^2+q^2 = 1 \)なので、\( |4p-1| = 2 \)
\( 4p-1 = ±2 \)
\( 4p = 3, -1 \)より、\( \displaystyle p = \frac{3}{4}, -\frac{1}{4} \)
\( \displaystyle p = \frac{3}{4} \)の場合、これをDに代入すると、\( \displaystyle \left(\frac{3}{4}\right)^2+q^2 = 1 \)より、
\( \displaystyle q^2 = \frac{7}{16} \)なので、\( \displaystyle q = ±\frac{\sqrt{7}}{4} \)
\( \displaystyle p = -\frac{1}{4} \)の場合、これをDに代入すると、\( \displaystyle \left(-\frac{1}{4}\right)^2+q^2 = 1 \)より、
\( \displaystyle q^2 = \frac{15}{16} \)なので、\( \displaystyle q = ±\frac{\sqrt{15}}{4} \)
Cにこの値を代入すればいいので、求める接線の方程式はすべてで\( \displaystyle \frac{3}{4}x+\frac{\sqrt{7}}{4}y = 1 \),\( \displaystyle \frac{3}{4}x-\frac{\sqrt{7}}{4}y = 1 \),\( \displaystyle -\frac{1}{4}x+\frac{\sqrt{15}}{4}y = 1 \),\( \displaystyle -\frac{1}{4}x-\frac{\sqrt{15}}{4}y = 1 \)の4つです。
(別解)
接線の方程式の公式を使わずに解くこともできます。その場合、このように場合分けして考える必要があります。
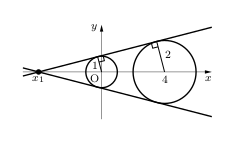
(i)右の図のようにひくことができる接線が2本考えられます。このとき、点$x_1$と円の中心、接点の3点でできる三角形が円①と円②のそれぞれでできますね?その三角形どうしは相似の関係になるので、次のような比が成り立ちます。
\( (0-x_1):(4-x_1) = 1:2 \)
\( -x_1:(4-x_1) = 1:2 \)
\( -2x_1 = 4-x_1 \)
\( -x_1 = 4 \)
\( ∴x_1 = -4 \)
つまり、接線は点\( (-4,0) \)を通るということになります。点\( (a,b) \)を通り、傾きが$m$である直線の方程式は\( y-b = m(x-a) \)と表せますから、接線の方程式は\( y = m(x+4) \)とおけます。あとは$m$を求めるだけになりますね?
ここで、さっきの解説にもあったとおり、直線が円に接するということは、直線と円の中心との距離がそのまま円の半径になっているわけです。円①の中心は\( (0,0) \)で半径は1、そして接線の方程式は\( mx-y+4m = 0 \)と変形できるので、
\( \displaystyle \frac{|4m|}{\sqrt{m^2+(-1)^2}} = 1 \)
これを解いていくと、\( |4m| = \sqrt{m^2+1} \)
両辺を2乗して、\( 16m^2 = m^2+1 \)
\( 15m^2 = 1 \)
\( \displaystyle m^2 = \frac{1}{15} \)
\( \displaystyle m = ±\frac{1}{\sqrt{15}} \)
よって、さっきの図の2本の接線の方程式は\( \displaystyle y = ±\frac{1}{\sqrt{15}}(x+4) \)です。
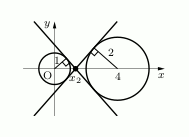
(ii)ほかにも、右の図のようにひくことができる接線も2本考えられます。この場合でも、点$x_2$と円の中心、接点の3点でできる三角形が円①と円②のそれぞれでできますね?その三角形どうしは相似の関係になるので、次のような比が成り立ちます。
\( x_2:(4-x_2) = 1:2 \)
\( 2x_2 = 4-x_2 \)
\( 3x_2 = 4 \)
\( \displaystyle ∴x_2 = \frac{4}{3} \)
よって、(i)と同様に考えれば、接線の方程式は\( \displaystyle y = m\left(x-\frac{4}{3}\right) \)とおけて、円①の中心である\( (0,0) \)からの距離が1となるので、
\( \displaystyle \frac{|-\frac{4}{3}m|}{\sqrt{m^2+(-1)^2}} = 1 \)
これを解いていくと、\( \displaystyle \left|-\frac{4}{3}m\right| = \sqrt{m^2+1} \)
両辺を2乗して、\( \displaystyle \frac{16}{9}m^2 = m^2+1 \)
\( 16m^2 = 9m^2+9 \)
\( 7m^2 = 9 \)
\( \displaystyle m^2 = \frac{9}{7} \)
\( \displaystyle m = ±\frac{3}{\sqrt{7}} \)
よって、この場合の2本の接線の方程式は\( \displaystyle y = ±\frac{3}{\sqrt{7}}\left(x-\frac{4}{3}\right) \)です。
(i),(ii)より、求める接線の方程式はすべてで\( \displaystyle y = ±\frac{1}{\sqrt{15}}(x+4) \),\( \displaystyle y = ±\frac{3}{\sqrt{7}}\left(x-\frac{4}{3}\right) \)です。
答え.
(1)
\( k<0,3<k \)
(2)
\( \displaystyle -1<k<-\frac{1}{5} \)
(3)
\( \displaystyle \frac{3}{4}x+\frac{\sqrt{7}}{4}y = 1 \),\( \displaystyle \frac{3}{4}x-\frac{\sqrt{7}}{4}y = 1 \),\( \displaystyle -\frac{1}{4}x+\frac{\sqrt{15}}{4}y = 1 \),\( \displaystyle -\frac{1}{4}x-\frac{\sqrt{15}}{4}y = 1 \)
(\( \displaystyle y = ±\frac{1}{\sqrt{15}}(x+4) \),\( \displaystyle y = ±\frac{3}{\sqrt{7}}\left(x-\frac{4}{3}\right) \)としてもOK)