この問題のポイント
2次式について、「ここからここまでの区間の積分をする」となったときは公式が使える!
(1)まず、$C_2$の方程式について、$C_1$を$x$軸方向へ$a$だけ平行移動したので、
\( y = (x-a)^3-3(x-a) \)とおけます。
このグラフと$C_1$が異なる2点で交わるならば、
\( (x-a)^3-3(x-a) = x^3-3x \)
\( x^3-3ax^2+3a^2x-a^3-3x+3a = x^3-3x \)
\( -3ax^2+3a^2x-a^3+3a = 0 \)
\( a \neq 0 \)より、\( 3x^2-3ax+a^2-3 = 0 \) …①
この方程式が異なる2つの解を持つこととなります。
よって、この方程式の判別式\( D = (-3a)^2-4・3・(a^2-3)>0 \)
\( 9a^2-12a^2+36>0 \)
\( -3a^2+36>0 \)
\( a^2-12<0 \)
\( -2\sqrt{3}<a<2\sqrt{3} \)
ただし、問題文より$a>0$なので、求める$a$の範囲は\( 0<a<2\sqrt{3} \)です。
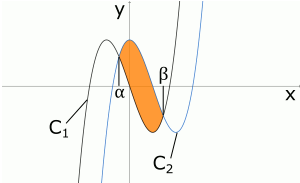
次に、面積$S(a)$についてです。面積は(上のグラフ)-(下のグラフ)の定積分を計算すれば求めることができますね?右の図より、この問題では上のグラフは青い曲線の$C_2$で、下のグラフは黒い曲線の$C_1$です。図のように、$C_1$と$C_2$の2つの交点の$x$座標をそれぞれ$α$,$β$($α<β$)とおくとします。①の方程式を$x$について解くと、
\( \displaystyle x = \frac{-(-3a)±\sqrt{(-3a)^2-4・3・(a^2-3)}}{2・3} \)
\( \displaystyle x = \frac{3a±\sqrt{-3a^2+36}}{6} = \frac{3a±\sqrt{36-3a^2}}{6} \)
よって、\( \displaystyle α = \frac{3a-\sqrt{36-3a^2}}{6} \),\( \displaystyle β = \frac{3a+\sqrt{36-3a^2}}{6} \)ですが、この値を使って積分の計算をするのはとても大変です。そこで、この公式を使うことにしましょう。
\( ●x^2+▲x+■ \)の形の式(つまり二次式)が\( (x-α)(x-β) \)に因数分解でき、さらにその$α$と$β$の区間で積分するとき、
\( \displaystyle \int_α^β (x-α)(x-β)dx = -\frac{1}{6}(β-α)^3 \)
これを使うと、今回の問題のような、ややこしい積分の計算がとても簡単になります。また、大学入試ではこの公式を利用しないと解くことが困難な問題も見受けられるので、必ずこの公式はマスターしておきましょう。
今回の問題について、
\( β-α \)
\( \displaystyle = \frac{3a+\sqrt{36-3a^2}}{6}-\frac{3a-\sqrt{36-3a^2}}{6} \)
\( \displaystyle = \frac{3a+\sqrt{36-3a^2}-(3a-\sqrt{36-3a^2})}{6} \)
\( \displaystyle = \frac{2\sqrt{36-3a^2}}{6} \)
\( \displaystyle = \frac{\sqrt{36-3a^2}}{3} \)
これより、
\( S(a) \)
\( \displaystyle = \int_α^β \{(x-a)^3-3(x-a)-(x^3-3x)\}dx \)
\( \displaystyle = \int_α^β \{x^3-3ax^2+3a^2x-a^3-3x+3a-(x^3-3x)\}dx \)\( \displaystyle = \int_α^β \{x^3-3ax^2+3a^2x-a^3-3x+3a \\ -(x^3-3x)\}dx \)
\( \displaystyle = \int_α^β (-3ax^2+3a^2x-a^3+3a)dx \)
\( \displaystyle = -3a\int_α^β (x-α)(x-β)dx \)
\( \displaystyle = -3a・\left\{-\frac{1}{6}(β-α)^3\right\} \)
\( \displaystyle = \frac{1}{2}a・\left(\frac{\sqrt{36-3a^2}}{3}\right)^3 \)
\( \displaystyle = \frac{1}{2}a・\left(\frac{\sqrt{3(12-a^2)}}{3}\right)^3 \)
\( \displaystyle = \frac{1}{2}a・\frac{3\sqrt{3}\sqrt{(12-a^2)^3}}{27} \)
\( \displaystyle = \frac{\sqrt{3}}{18}a\sqrt{(12-a^2)^3} \)
(別解)
\( β-α \)の値について、方程式①を直接解いて$α$と$β$の値を求めて計算するという方法で上では解きましたが、方程式を解かずに解と係数の関係を使って求めるという方法もあります。
方程式①について、解と係数の関係より、
\( \displaystyle α+β = -\frac{-3a}{3} = a \)
\( \displaystyle αβ= \frac{a^2-3}{3} \)
よって、
\( (β-α)^2 \)
\( = β^2-2αβ+α^2 \)
\( = α^2+β^2-2αβ \)
\( = (α+β)^2-2αβ-2αβ \)
\( = (α+β)^2-4αβ \)
\( \displaystyle = a^2-4・\frac{a^2-3}{3} \)
\( \displaystyle = \frac{3a^2-4(a^2-3)}{3} \)
\( \displaystyle = \frac{12-a^2}{3} \)
2つの交点の$x$座標を$α$,$β$としたときに$α<β$としたので、$β-α>0$なので、
\( β-α \)
\( \displaystyle = \sqrt{\frac{12-a^2}{3}} \)
\( \displaystyle = \frac{\sqrt{12-a^2}}{\sqrt{3}} \)
\( \displaystyle = \frac{\sqrt{3}\sqrt{12-a^2}}{3} \)
\( \displaystyle = \frac{\sqrt{36-3a^2}}{3} \)
あとはさっきのように、\( S(a) \)を求める過程で面積公式を使うときに、\( β-α \)のこの値を代入すれば同じように求まります。
(2)\( \displaystyle S(a) = \frac{\sqrt{3}}{18}a\sqrt{(12-a^2)^3} \)と求まりましたが、文字が根号(ルート)の中にあるものと外にあるものが混在しているので、全部根号の中にひとまず入れます。
すると、\( \displaystyle S(a) = \frac{\sqrt{3}}{18}\sqrt{a^2(12-a^2)^3} \)とおけます。
根号の中の最大値を考えればよいことになりますが、ふつうに$a$についての関数として見て展開していくと5乗などになるものも出てしまい、最大値を考えることができなくなってしまいます。そこで、\( 12-a^2 = t \)とおいてみましょう。すると、\( a^2 = 12-t \)ですから、\( \displaystyle S(a) = \frac{\sqrt{3}}{18}\sqrt{(12-t)t^3} \)とおけます。
ここで、根号の中身だけ取り出して\( f(t) = (12-t)t^3 \)とおきます。\( f(t) = 12t^3-t^4 \)なので、
\( f'(t) = 36t^2-4t^3 = 4t^2(9-t) \)
そして、$t$の範囲については、(1)より\( 0<a<2\sqrt{3} \)なので、
\( 0<a^2<12 \)のため、\( -12<-a^2<0 \)
これより、\( 0<-a^2+12<12 \)とわかるので、\( 0<t<12 \)です。
この範囲で増減表を書くと、このようになりますね。
| $t$ | 0 | … | 9 | … | 12 |
| $f'(t)$ | 0 | + | 0 | - | |
| $f(t)$ | 0 | ↗ | ↘ |
この増減表より、$t = 9$のときに最大値をとるとわかります。そのときの$S(a)$の値は、
\( S(a) \)
\( \displaystyle = \frac{\sqrt{3}}{18}\sqrt{f(9)} \)
\( \displaystyle = \frac{\sqrt{3}}{18}\sqrt{(12-9)・9^3} \)
\( \displaystyle = \frac{\sqrt{3}}{18}・27\sqrt{3} \)
\( \displaystyle = \frac{9}{2} \)
答え.
(1)$a$の範囲は\( 0<a<2\sqrt{3} \),\( \displaystyle S(a) = \frac{\sqrt{3}}{18}a\sqrt{(12-a^2)^3} \)
(2)\( \displaystyle \frac{9}{2} \)