この問題のポイント
sinとcosをたした形の式はsin(θ+α)の形に変形することができる!
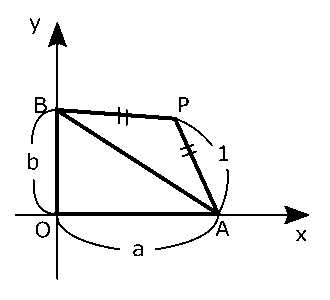
$P$の位置は直線$AB$に関して$O$と反対側にある場合と同じ側にある場合の2通りが考えられますが、この問題では$S$が最大となるときを考えるので、$P$は直線$AB$に関して$O$と反対側にある場合だけを考えればいいですね?よって、問題の状況を図にすると右の図のようになります。
(1)〈指針〉
$S$の図形は$△OAB$と$△PAB$を合わせた形です。$∠APB$は固定されていますから、$△PAB$の面積は一定です。よって、$△OAB$の面積が最大になるのはどういうときかを考えていくことで$a = b$であることを証明していきます。いろいろな方法で証明できますが、この解説では相加平均・相乗平均の関係を使って証明します。
$x = y$については、$P$の座標が関係していますから$△PAB$に着目して考えることができます。\( PA = PB = 1 \)なので、これを利用して$x = y$を導くといいでしょう。
〈証明〉
\( S = △OAB+△PAB \)であり、$∠APB$は固定されているので、$△PAB$の面積は一定であるため、$△OAB$の面積が最大であるときを考える。
$△OAB$の面積は\( \displaystyle \frac{1}{2}OA・OB = \frac{1}{2}ab \)である。
ここで、$∠APB$は固定されているので、$AB$の長さも一定である。\( AB = \sqrt{a^2+b^2} \)が一定という条件のもとで\( \displaystyle \frac{1}{2}ab \)が最大となるときを考える。
$a^2$と$b^2$について、相加平均・相乗平均の関係より、
\( \displaystyle \frac{a^2+b^2}{2}≧\sqrt{a^2+b^2} \)
$a>0$,$b>0$より、\( \displaystyle \frac{a^2+b^2}{2}≧ab \)
この等号が成立するときは、\( a^2 = b^2 \)、つまり\( a = b \)のときなので、$△OAB$の面積である\( \displaystyle \frac{1}{2}ab \)が最大となるのは\( a = b \)のときである。
また、\( PA = PB \)なので、\( PA^2 = PB^2 \)である。
よって、\( (x-a)^2+y^2 = x^2+(y-b)^2 \)
\( x^2-2ax+a^2+y^2 = x^2+y^2-2by+b^2 \)
\( -2ax+a^2 = -2by+b^2 \)
\( 2ax-a^2 = 2by-b^2 \)
$S$が最大のとき\( a = b \)なので、\( 2ax-a^2 = 2ay-a^2 \)となるため、\( 2ax = 2ay \)
\( a \neq 0 \),\( b \neq 0 \)なので、\( x = y \)である。
(別解)
〈指針〉にて\( a = b \)を示す方法はいろいろあると書きましたが、その一つに、$△OAB$の面積を三角比を使ってあらわし、その最大値を考えるという方法があります。
$∠OAB = α$とおくと、
\( \displaystyle △OAB = \frac{1}{2}OA・OB \)
\( \displaystyle = \frac{1}{2}AB\cosα・AB\sinα \)
\( \displaystyle = \frac{1}{2}AB^2\cosα・\sinα \)
2倍角の公式を利用すると、\( \displaystyle △OAB = \frac{1}{4}AB^2\sin{2α} \)
ここで、\( \displaystyle 0<α<\frac{π}{2} \)より、\( 0<2α<π \)
この範囲で\( \sin{2α} \)が最大となるのは\( \displaystyle 2α = \frac{π}{2} \)のとき、つまり\( \displaystyle α = \frac{π}{4} \)のときである。
このとき、\( \displaystyle OA = AB\cos{\frac{π}{4}} = \frac{\sqrt{2}}{2}AB \)
よって、\( \displaystyle a = \frac{\sqrt{2}}{2}AB \)
\( \displaystyle OB = AB\sin{\frac{π}{4}} = \frac{\sqrt{2}}{2}AB \)
よって、\( \displaystyle b = \frac{\sqrt{2}}{2}AB \)
どちらも\( \displaystyle \frac{\sqrt{2}}{2}AB \)なので\( a = b \)
(\( x = y \)についてはさきほどと同じやりかたで証明することができます。)
(2)さっきの(1)にて考えたとおり、$△OAB$の面積は\( \displaystyle \frac{1}{2}ab \)と表せます。そして、$∠APB = θ$とおくと、$△PAB$の面積は
\( \displaystyle \frac{1}{2}・1・1・\sinθ = \frac{1}{2}\sinθ \)
ここで、\( a = b \)という条件があるのですから、(1)で考えた相加平均・相乗平均の関係での等号が成立します。
つまり、\( \displaystyle \frac{a^2+b^2}{2} = ab \)となるので、$△OAB$の面積は\( \displaystyle \frac{1}{2}・\frac{a^2+b^2}{2} = \frac{a^2+b^2}{4} \)と表せます。
\( a^2+b^2 \)という式を見ると、これは(1)にて考えた$AB$の長さの2乗に等しいです。ちょうど$∠APB = θ$とおいているので、$△PAB$において余弦定理を使って$AB$を表してみると、
\( AB^2 = AP^2+BP^2-2AP・BP・\cos{∠APB} \)
\( AB^2 = 1^2+1^2-2・1・1・\cosθ \)
\( ∴a^2+b^2 = 2-2\cosθ \)
よって、$△OAB$の面積は\( \displaystyle \frac{2-2\cosθ}{4} = \frac{1-\cosθ}{2} \)なので、$S$の面積は
\( \displaystyle \frac{1-\cosθ}{2}+\frac{1}{2}\sinθ \)
\( \displaystyle = \frac{1}{2}\sinθ-\frac{1}{2}\cosθ+\frac{1}{2} \)
\( \displaystyle = \frac{1}{2}(\sinθ-\cosθ)+\frac{1}{2} \) …①です。
この最大値について考えるわけですが、この式では\( \sinθ \)と\( \cosθ \)の両方が混じっていて考えづらいです。そこで、三角関数の合成を使って式を変形させます。三角関数の合成とは次のような変形のことをいいます。
\( a\sinθ+b\cosθ = \sqrt{a^2+b^2}\sin{(θ+α)} \)に書き換えることを三角関数の合成という。
(ただし、\( \displaystyle \cosα = \frac{a}{\sqrt{a^2+b^2}} \),\( \displaystyle \sinα = \frac{b}{\sqrt{a^2+b^2}} \)とする。)
(証明)
\( a\sinθ+b\cosθ \)
\( \displaystyle = \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sinθ+\frac{b}{\sqrt{a^2+b^2}}\cosθ\right) \)
\( \displaystyle = \sqrt{a^2+b^2}\left(\sinθ\frac{a}{\sqrt{a^2+b^2}}+\cosθ\frac{b}{\sqrt{a^2+b^2}}\right) \)
ここで、\( \displaystyle \cosα = \frac{a}{\sqrt{a^2+b^2}} \),\( \displaystyle \sinα = \frac{b}{\sqrt{a^2+b^2}} \)とすると、
\( \sqrt{a^2+b^2}(\sinθ\cosα+\cosθ\sinα) \)となる。
よって、加法定理より、\( \sqrt{a^2+b^2}\sin{(θ+α)} \)とできる。
これより、①の式にある\( \sinθ-\cosθ \)を合成すると、
\( \displaystyle \sqrt{1^2+1^2}\left(\frac{1}{\sqrt{1^2+1^2}}\sinθ-\frac{1}{\sqrt{1^2+1^2}}\cosθ\right) \)
\( \displaystyle = \sqrt{2}\left(\frac{1}{\sqrt{2}}\sinθ-\frac{1}{\sqrt{2}}\cosθ\right) \)
\( \displaystyle = \sqrt{2}\sin{\left(θ-\frac{π}{4}\right)} \)
よって、$S$を示す①の式は\( \displaystyle \frac{\sqrt{2}}{2}\sin{\left(θ-\frac{π}{4}\right)}+\frac{1}{2} \)ということになります。
\( 0<θ<π \)ですから、\( \displaystyle -\frac{π}{4}<θ-\frac{π}{4}<\frac{3}{4}π \)なので、\( \displaystyle θ-\frac{π}{4} = \frac{π}{2} \)、つまり\( \displaystyle θ = \frac{3}{4}π \)のときにこの式の値は最大となります。
その式の値は\( \displaystyle \frac{\sqrt{2}}{2}・1+\frac{1}{2} \)、つまり\( \displaystyle \frac{\sqrt{2}+1}{2} \)です。
答え.
(1)(上の〈証明〉や(別解)参照)
(2)\( \displaystyle \frac{\sqrt{2}+1}{2} \)