この問題のポイント
つなぎの文字を消去してxとyだけであらわした式をつくる!
中点の座標を考えるときは解と係数の関係を使うと便利!
(1)$P$,$Q$は$C_1$と$C_2$の2つの円の交点ですから、$C_1$の方程式がどのようなものかを明らかにしないと考えることができません。よって、まずはそれを考えていきましょう。
$C_1$の中心は\( (2,t) \)で、この円は\( O(0,0) \)を通るわけですから、
半径は\( \sqrt{(2-0)^2+(t-0)^2} = \sqrt{4+t^2} \)
よって、円$C_1$の方程式は
\( (x-2)^2+(y-t)^2 = (\sqrt{4+t^2})^2 \)
\( (x-2)^2+(y-t)^2 = 4+t^2 \)
\( x^2-4x+4+y^2-2ty+t^2 = 4+t^2 \)
\( x^2-4x+y^2-2ty = 0 \)…①
これと\( x^2+y^2 = 4 \)…②の交点ですから、②を①に代入して、
\( 4-4x-2ty = 0 \)…③
これを$t$について整理すると\( -2y・t+(4-4x) = 0 \)
$t$の値にかかわらずこの式がつねに成立するようになるには、\( -2y = 0 \),\( 4-4x = 0 \)の両方が成立すればいいということになります。
解くと\( y = 0 \),\( x = 1 \)より、$t$の値にかかわらず(1,0)を通るということになります。
(2)$P$,$Q$の座標をそれぞれ\( (x_1,y_1) \),\( (x_2,y_2) \)とします。このそれぞれの値を求めるには、①と②の連立方程式を解かないといけません。その過程でできた式が③ですが、③より、
\( 4x = 4-2ty \)なので、\( \displaystyle x = 1-\frac{1}{2}ty \)…④
これを②に代入すると、
\( \displaystyle (1-\frac{1}{2}ty)^2+y^2 = 4 \)
\( \displaystyle 1-ty+\frac{1}{4}t^2y^2+y^2 = 4 \)
\( \displaystyle \left(\frac{1}{4}t^2+1\right)y^2-ty-3 = 0 \)
この方程式を解くと$y_1$や$y_2$の値が求まりますが、なかなか大変そうです。そもそも$R$は線分$PQ$の中点ですから、$R$の$y$座標は\( \displaystyle \frac{y_1+y_2}{2} \)ですので、$y_1+y_2$の値さえわかればいいはずです。このような場合には解と係数の関係を使うとラクに計算することができます。
解と係数の関係より、$y_1+y_2$は、
\( \displaystyle -\frac{-t}{\displaystyle\frac{1}{4}t^2+1} \)
\( \displaystyle = t÷\left(\frac{1}{4}t^2+1\right) \)
\( \displaystyle = t÷\frac{t^2+4}{4} \)
\( \displaystyle = t×\frac{4}{t^2+4} \)
\( \displaystyle = \frac{4t}{t^2+4} \)
$R$の$y$座標は\( \displaystyle \frac{y_1+y_2}{2} \)ですので、\( \displaystyle \frac{2t}{t^2+4} \)とわかります。$R$の$x$座標は④より
\( \displaystyle 1-\frac{1}{2}t・\frac{2t}{t^2+4} \)
\( \displaystyle = 1-\frac{t^2}{t^2+4} \)
\( \displaystyle = \frac{t^2+4}{t^2+4}-\frac{t^2}{t^2+4} \)
\( \displaystyle = \frac{4}{t^2+4} \)
よって、$R$の座標は\( \displaystyle \left(\frac{4}{t^2+4},\frac{2t}{t^2+4}\right) \)
(3)\( \displaystyle x = \frac{4}{t^2+4} \),\( \displaystyle y = \frac{2t}{t^2+4} \)とおきます。この$t$を消去するようにしていくと、$x$と$y$だけの式にできそうですね?
\( \displaystyle x = \frac{4}{t^2+4} \)より、\( (t^2+4)x = 4 \)
$t^2>0$より$t^2+4>0$なので、$x>0$といえますから両辺を$x$で割ると、\( \displaystyle t^2+4 = \frac{4}{x} \)
\( \displaystyle ∴t^2 = \frac{4}{x}-4 \)
そして、\( \displaystyle y = \frac{2t}{t^2+4} \)なので、
\( (t^2+4)y = 2t \)
\( \displaystyle \left(\frac{4}{x}-4+4\right)y = 2t \)
\( \displaystyle \frac{4}{x}・y = 2t \)
\( \displaystyle \frac{16}{x^2}・y^2 = 4t^2 \)
\( \displaystyle \frac{16}{x^2}・y^2 = 4\left(\frac{4}{x}-4\right) \)
\( \displaystyle \frac{16}{x^2}・y^2 = \frac{16}{x}-16 \)
\( 16y^2 = 16x-16x^2 \)
\( 16x^2-16x+16y^2 = 0 \)
\( x^2-x+y^2 = 0 \)
\( \displaystyle x^2-x+\frac{1}{4}+y^2 = \frac{1}{4} \)
\( \displaystyle \left(x-\frac{1}{2}\right)^2+y^2 = \frac{1}{4} \)
これは中心が\( \displaystyle \left(\frac{1}{2},0\right) \)で半径が\( \displaystyle \frac{1}{2} \)の円をあらわしていますね?ただし、軌跡の問題では、その図形上のすべての点が本当に問題文に書かれた条件を満たすのかを確認しなければなりません。
この問題を解く過程で$x>0$ということを確認しました。しかし、\( \displaystyle \left(x-\frac{1}{2}\right)^2+y^2 = \frac{1}{4} \)の円は$x = 0$のとき$y = 0$となるので(0,0)の点(原点)を通ります。この点だけは問題文の条件には合わないはずなので、この点は除外されるべきということになります。
よって、求める軌跡は、中心が\( \displaystyle \left(\frac{1}{2},0\right) \)で半径が\( \displaystyle \frac{1}{2} \)の円で原点を除いたものということになります。
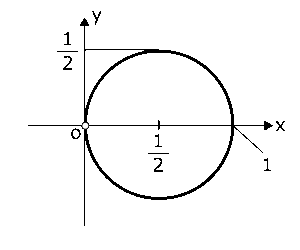
答え.
(1)(1,0)
(2)\( \displaystyle \left(\frac{4}{t^2+4},\frac{2t}{t^2+4}\right) \)
(3)中心が\( \displaystyle \left(\frac{1}{2},0\right) \)で半径が\( \displaystyle \frac{1}{2} \)の円で原点を除いたもの。図示したものは右の図。