この問題のポイント
関数y = f(x)上の点(a,f(a))における接線の傾きはf'(a)!
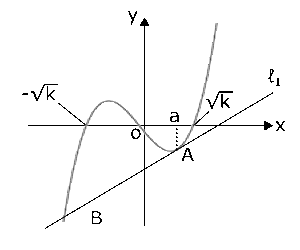
(1)問題に書かれていることを図にすると、右の図のようになります。まず$l_1$の方程式がわからないと、$B$の座標を求めにくそうですから、$l_1$の方程式を考えてみましょう。
$l_1$は$C$の接線ですが、関数のグラフの接線について、上の「この問題のポイント」にあるとおり、\( y = f(x) \)上の点\( (a,f(a)) \)における接線は傾きの値が$f'(a)$となります。つまり、微分して$x$座標の数値を入れて計算したら、接線の傾きの値が求まるということです。
これを利用して、$l_1$の傾きを求めます。$C$の関数は\( y = x^3-kx \)ですから、\( y' = 3x^2-k \)
よって、点$A$の$x$座標は$a$なので、接線$l_1$の傾きは\( 3a^2-k \)
また、「図形と方程式」の単元で学んだとおり、点\( (A,B) \)を通って傾きが$m$の直線の方程式は\( y-B = m(x-A) \)と表せるんでしたね?$l_1$は\( (a,a^3-ka) \)を通って、傾きが\( 3a^2-k \)なので、$l_1$の方程式は、
\( y-(a^3-ka) = (3a^2-k)(x-a) \)
\( y = (3a^2-k)(x-a)+a^3-ka \)
\( y = (3a^2-k)x-3a^3+ka+a^3-ka \)
\( y = (3a^2-k)x-2a^3 \)
$l_1$の方程式が求まりました。これより、$l_1$と$C$の交点の$x$座標は
\( (3a^2-k)x-2a^3 = x^3-kx \)
\( x^3-3a^2x+2a^3 = 0 \)
\( (x-a)^2(x+2a) = 0 \)
\( x= a,-2a \)
$A$の$x$座標が$a$なので、$B$の$x$座標は$-2a$です。
(2)$C$の方程式を微分したら\( y' = 3x^2-k \)で、(1)より$B$の$x$座標は$-2a$なんですから、$B$における接線の傾きは
\( 3・(-2a)^2-k = 12a^2-k \)
$l_1$と$l_2$が垂直に交わるということですが、垂直に交わる2つの直線は、それぞれの傾きの値をかけると-1になるんですから、
\( (3a^2-k)(12a^2-k) = -1 \)
これがこの問題で求める条件となるわけですが、もう少し整理していきます。
\( 36a^4-3ka^2-12ka^2+k^2 = -1 \)
\( 36a^4-15ka^2+k^2+1 = 0 \)…①
(3)(2)で求めた条件が成立すればいいので、①の方程式を満たす$a$が存在すればいいということになります。ただし、①は4次方程式となって少し考えにくいので、\( a^2 = t \)と置き換えて、
\( 36t^2-15kt+k^2+1 = 0 \)とします。
この2次方程式が\( t≧0 \)の実数解をもてばいいはずですね?($t$は$a^2$を置き換えたものなので、負の数になってはいけません)。その条件を考えていきましょう。
まず、判別式$D$は0以上でないといけませんので、
\( D = (-15k)^2-4・36・(k^2+1)≧0 \)
\( 225k^2-144k^2-144≧0 \)
\( 25k^2-16k^2-16≧0 \)
\( 9k^2≧16 \)
\( \displaystyle k^2≧\frac{16}{9} \)
\( \displaystyle ∴k≦-\frac{4}{3},\frac{4}{3}≦k \)…②
そして、\( f(t) = 36t^2-15kt+k^2+1 \)とすると、\( f(0) = k^2+1 \)で、この値は必ず正の数になるので、\( t≧0 \)の実数解をもつには$f(t)$をグラフにした放物線の軸が正のところにある必要があります。
\( f(t) = 36t^2-15kt+k^2+1 \)
\( \displaystyle = 36(t^2-\frac{5}{12}kt)+k^2+1 \)
\( \displaystyle = 36(t^2-\frac{5}{12}kt+\frac{5^2}{24^2}k^2-\frac{5^2}{24^2}k^2)+k^2+1 \)
\( \displaystyle = 36(t^2-\frac{5}{12}kt+\frac{5^2}{24^2}k^2)-36・\frac{5^2}{24^2}k^2+… \)
\( \displaystyle = 36(t^2-\frac{5}{24}k)^2-… \)なので、軸\( \displaystyle \frac{5}{24}k≧0 \)となればいいので、\( k≧0 \)…③
②と③両方を満たす範囲は\( \displaystyle k≧\frac{4}{3} \)です。
(別解)
放物線の軸を考える代わりに、解と係数の関係を使って考えてもよいでしょう。$f(0)$は必ず正の数になるので、\( t≧0 \)の実数解をもつときは2つの解とも正の数になるはずです。つまり、2つの解を$α$,$β$とおくと、
\( α+β≧0 \)かつ\( \displaystyle αβ≧0 \)が成り立ちます。
解と係数の関係より、\( \displaystyle α+β = \frac{15k}{36}≧0 \)
これを解くと、\( k≧0 \)
\( \displaystyle αβ = \frac{k^2+1}{36}≧0 \)
しかし、これは\( k^2+1≧0 \)ということであり、kがどのような実数でも成立します。
よって、\( k≧0 \)と②の両方を満たす範囲を考えることになるので、\( \displaystyle k≧\frac{4}{3} \)と求まります。
答え.
(1)$-2a$
(2)\( 36a^4-15ka^2+k^2+1 = 0 \)
(3)\( \displaystyle k≧\frac{4}{3} \)