この問題のポイント
等差数列と等比数列それぞれについて、3項の関係、一般項の求め方、和の求め方をおさえる!
(1)$\{x_n\}$と$\{y_n\}$について、「このように3項が並んでいる」というのが示されています。これだけのことから、次の公式を使って、式を導き出すことができます。
$A$,$B$,$C$が等差数列なら
\( 2B = A+C \)
(証明)
等差数列ということは、公差が等しいので、
\( B-A = C-B \)
\( B+B = A+C \)
\( ∴2B = A+C \)
$A$,$B$,$C$が等比数列なら
\( B^2 = AC \)
(証明)
等比数列ということは、公比が等しいので、
\( \displaystyle \frac{B}{A} = \frac{C}{B} \)
両辺にABをかけると\( B^2 = AC \)
この公式を利用すると、まず$\{x_n\}$は$a$,$b$,$c$という等差数列なので、
\( 2b = a+c \) …①
$\{y_n\}$は$c$,$a$,$b$という等比数列なので、
\( a^2 = bc \) …②
①を変形すると、\( c = 2b-a \) …③
これを②に代入すると、
\( a^2 = b(2b-a) \)
\( a^2 = 2b^2-ab \)
\( a^2+ab-2b^2 = 0 \)
因数分解すると、\( (a+2b)(a-b) = 0 \)
これを解くと、\( \displaystyle b = -\frac{1}{2}a,a \)
しかし、$a$,$b$,$c$は相異なる実数ですから、\( b \neq a \)より、
\( \displaystyle b = -\frac{1}{2}a \)
これを③に代入すると、
\( \displaystyle c = 2・\left(-\frac{1}{2}a\right)-a = -2a\)
よって、公差は、
\( \displaystyle b-a = -\frac{1}{2}a-a = -\frac{3}{2}a \)
(2)$\{y_n\}$のはじめは$-2a$,$a$,\( \displaystyle -\frac{1}{2}a \)なので、$\{y_n\}$の公比は\( \displaystyle -\frac{1}{2} \)です。
そして、等差数列と等比数列について、初項から第$n$項までの和は次の公式で求めることができます。
等差数列
初項が$a_1$、$n$番目の項が$a_n$とすると、
\( \displaystyle \frac{1}{2}n(a_1+a_n) \)
等比数列
初項が$a_1$、$n$番目の項が$a_n$、公比が$r$とすると、\( r \neq 1 \)ならば
\( \displaystyle \frac{a_1(1-r^n)}{1-r} = \frac{a_1(r^n-1)}{r-1} \)
$r = 1$ならば$na_1$
この公式を使うと、$\{y_n\}$の初項から第8項までの和は、
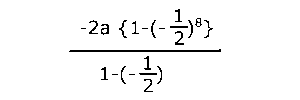
これを計算していくと、
\( \displaystyle \left(-2a・\frac{255}{256}\right)÷\frac{3}{2} \)
\( \displaystyle = -\frac{255}{128}a×\frac{2}{3} \)
\( \displaystyle = -\frac{85}{64}a \)
(3)$\{z_n\}$ = $b$,$c$,$a$,…で、
\( \displaystyle c-b = -2a-\left(-\frac{1}{2}a\right) = -\frac{3}{2}a \)
\( a-c = a-(-2a) = 3a \)
よって、\( \displaystyle \{w_n\} = -\frac{3}{2}a,3a,… \)
これが等差数列であるとするのですから、この数列の公差は
\( \displaystyle 3a-\left(-\frac{3}{2}a\right) = \frac{9}{2}a \)
そして、一般項のことが問題になっていますが、一般項を求める公式は次のようになっています。
等差数列
初項が$a_1$、公差を$d$とすると、
\( a_n = a_1+d(n-1) \)
等比数列
初項が$a_1$、公比が$r$とすると、
\( a_n = a_1・r^{n-1} \)
$\{w_n\}$の初項は\( \displaystyle -\frac{3}{2}a \)、公差は\( \displaystyle \frac{9}{2}a \)なので、
$w_n$
\( \displaystyle = -\frac{3}{2}a+\frac{9}{2}a(n-1) \)
\( \displaystyle = -\frac{3}{2}a+\frac{9}{2}an-\frac{9}{2}a \)
\( \displaystyle = \frac{9n-12}{2}a \)
答え.
アイ -1 ウ 2
エオ -2
カキ -3 ク 2
ケコサ -85 シス 64
セ 9 ソ 2
タ 9 チツ 12 テ 2