この問題のポイント
微分することと積分することは、互いに逆の計算をしていること!
$f(x)$を積分するということは、微分したら$f(x)$になる関数は何かを探すということです。なので、$f(x)$を積分して微分すると、また$f(x)$になるということであり、もっと簡単にいうと、微分と積分は逆の関係になっているということになります。
$F(x)$は$f(x)$を積分して求まった関数です。ということは、これを微分したらもとの関数にもどるんですから、\( F'(x) = f(x) \)となります。
$W$は$t>1$での$y = f(x)$,$x$軸(つまり$y = 0$),$x = 1$,$x = t$で囲まれた部分の面積です。$x≧1$の範囲ではつねに$f(x)≦0$ということは、つまり$f(x)$は$x$軸上か$x$軸より下にあるかということです。(上のグラフ)-(下のグラフ)を積分すれば面積が求まるんですから、
\begin{eqnarray} &&\int_1^t \{0-f(x)\}dx\\ &&= \int_1^t -f(x)dx\\ &&= -\int_1^t f(x)dx\\ &&= -\left[F(x)\right]_1^t\\ &&= -{F(t)-F(1)}\\ \end{eqnarray}
これより、\( W = -F(t)+F(1) \)です。
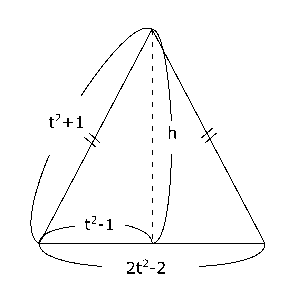
$W$は右の図にある二等辺三角形の面積とつねに等しいので、その面積を考えます。底辺は\( 2t^2-2 \)とわかっていますが、高さがわからないのでそれを$h$として求めることにすると、三平方の定理より、
\( (t^2-1)^2+h^2 = (t^2+1)^2 \)
\( t^4-2t^2+1+h^2 = t^4+2t^2+1 \)
\( h^2 = 4t^2 \)
$h>0$,$t>1$ですから、$h = 2t$
\( \small{(t^2-1)^2+h^2 = (t^2+1)^2} \)
\( \small{t^4-2t^2+1+h^2 = t^4+2t^2+1} \)
\( \small{h^2 = 4t^2} \)
$h>0$,$t>1$ですから、$h = 2t$
よって、面積は
\( \displaystyle \frac{1}{2}・(2t^2-2)・2t \)
\( = 2t^3-2t \)
これが$W$、つまり\( -F(t)+F(1) \)と等しいんですから、
\( -F(t)+F(1) = 2t^3-2t \) …A
さて、この問題では、最後に$f(t)$を求めなければなりませんが、$F(t)$は$f(t)$を積分して求まる関数です。ということは、$f(t)$を求めるには、$F(t)$を微分しなければなりませんね。よって、Aの式を微分すると、$f(t)$を求めることができます。
Aの式にある$F(1)$ですが、これは$t = 1$を代入した値になるわけですが、数値は微分すると0になりますから、Aの式を微分すると、
\( -f(t) = 6t^2-2 \)
よって、\( f(t) = -6t^2+2 \)
答え.
ツ ⑦ テ ④
トナ -6 ニ 2 ヌ 2