この問題のポイント
( )( ) = (整数)という式を導いて整数となる値を見つけよう!
条件が少ないときは解と係数の関係が利用できるときがある!
(1)$a = b$なので、\( x^2+ax+a = 0 \)、\( y^2+ay+a = 0 \)とおけます。これらの方程式は$x$と$y$の文字だけが変わっているだけなので、\( x^2+ax+a = 0 \)だけで考えることにし、この方程式の解を$A$,$B$とおきます。
$A$と$B$は整数ということがわかっていますから、それを利用して( )( ) = (整数)という式をつくると、何か解く手がかりが手に入れられそうですが、そのための材料が見つかりません。そこで、解と係数の関係を利用してその材料ができないか考えてみましょう。
解と係数の関係は次のようなものですね。
\( ax^2+bx+c = 0 \)の解を$α$,$β$とすると、
\( \displaystyle α+β = -\frac{b}{a} \)
\( \displaystyle αβ = \frac{c}{a} \)
これを利用すると、
\( A+B = -a \) …①
\( AB = a \) …②
②を①に代入すると、
\( A+B = -AB \)
\( AB+A+B = 0 \)
ここで、\( AB+A = A(B+1) \)となるので、もしこの式の左辺に+1があれば因数分解ができるようになります。そこで、式の両辺に+1を加えると、
\( AB+A+B+1 = 1 \)
\( A(B+1)+B+1 = 1 \)
\( (A+1)(B+1) = 1 \)
すると、さっき書いた( )( ) = (整数)の形がここでできました。$A$,$B$は整数なので、$A+1$,$B+1$も整数ですから、この掛け算が成り立つということは、
\( A+1 = 1 \),\( B+1 = 1 \)か\( A+1 = -1 \),\( B+1 = -1 \)となりますね。
\( A+1 = 1 \),\( B+1 = 1 \)のときは\( A = 0 \),\( B = 0 \)で、\( a = AB = 0 \)
\( A+1 = -1 \),\( B+1 = -1 \)のときは\( A = -2 \),\( B = -2 \)で、\( a = AB = 4 \)
$a>0$なんですから、条件に合うのは$a = 4$のみということになります。
(2)(1)のように( )( ) = (整数)の形をつくることに変わりはありませんが、$a$か$b$どちらかの文字を消去しないとやりにくいですから、まずそこから取り組みます。
\( x^2+ax+b = 0 \)の解を$C$,$D$とすると、解と係数の関係より、
\( C+D = -a \),\( CD = b \)
ここで、$a$も$b$も0より大きい数、つまり正の数なんですから、$-a<0$,$b>0$
これより、$C$と$D$を足したら負の数、かけたら正の数になるとわかるので、$C$と$D$は両方とも負の数ということになり、$C$と$D$は整数解なんですから、$C$と$D$は負の整数、つまり-1以下の整数だということになります。
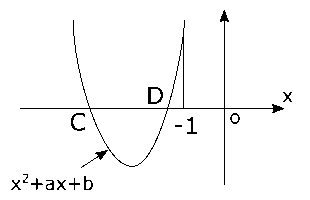
$C$と$D$が-1以下の整数ということは、\( x^2+ax+b \)に$x = -1$を代入した値は0以上になるはずです。なぜなら、\( f(x) = x^2+ax+b \)のグラフを描いて$C$と$D$が$x = -1$以下のところで交点になるには、右の図のようにならないといけないからです。
よって、
\( (-1)^2+a・(-1)+b \)
\( = -a+b+1≧0 \)
この式を変形すると、\( -a≧-b-1 \)
\( a≦b+1 \)
$a>b$ですから、$b<a≦b+1$ですが、$a$も$b$も整数なんですから、$a = b+1$にならないといけません。
よって、$a = b+1$ …③を\( y^2+by+a = 0 \)に代入すると、\( y^2+by+b+1 = 0 \)
この方程式の解を$E$,$F$($E≧F$)とすると、解と係数の関係より、
\( E+F = -b \),\( EF = b+1 \) …④
これより、\( b = -E-F \) …⑤より、これを\( EF = b+1 \)に代入すると、
\( EF = -E-F+1 \)
\( EF+E+F-1 = 0 \)
さっきのように、この式の左辺に+1があれば因数分解できますから、両辺に+1を加えると、
\( EF+E+F+1-1 = 1 \)
-1を移項して\( EF+E+F+1 = 2 \)
よって、\( (E+1)(F+1) = 2 \)
$E≦F$なんですから\( E+1≦F+1 \)で、$E$と$F$は整数解なんですから、この掛け算が成り立つということは、
\( E+1 = 1 \),\( F+1 = 2 \)か\( E+1 = -2 \),\( F+1 = -1 \)となりますね。
\( E+1 = 1 \),\( F+1 = 2 \)のときは\( E = 0 \),\( F = 1 \)
\( E+1 = -2 \),\( F+1 = -1 \)のときは\( E = -3 \),\( F = -2 \)
しかし、④より、$b$は正の数ですから、$-b<0$,$b+1>0$
ということは、$E$と$F$を足したら負の数、かけたら正の数だということなので、$E$も$F$も両方とも負の数になるわけですから、\( E = -3 \),\( F = -2 \)ということになります。
⑤より、\( b = -(-3)-(-2) = 3+2 = 5 \)
そして、③より、\( a = 5+1 = 6 \)
つまり、求める$(a,b)$は$(6,5)$のみということになります。
答え. (1)$a = 4$ (2)$(a,b) = (6,5)$