この問題のポイント
正規分布表の概念と見方に慣れよう!
信頼区間の公式を使えるようになろう!
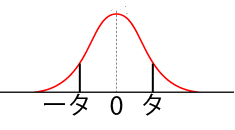
(1)\( P(-\fbox{タ}≦Z≦\fbox{タ}) \)というのは、正規分布のグラフを使って図示すると、右の図で黒の縦線ではさまれた部分ということになります。これが0.99だということは、その部分の面積が0.99だということになるわけです。
ただ、正規分布のグラフを見てわかるとおり、このグラフは0のところを軸として線対称になっています。ということは、\( P(-\fbox{タ}≦Z≦0) \)と\( P(0≦Z≦\fbox{タ}) \)の部分では面積は同じなので、\( P(0≦Z≦\fbox{タ}) \)の部分の面積が0.99の半分、つまり0.495であればよいと考えることができます。
正規分布表は、0のところからの部分の面積を示した表です。この問題では、0のところからタまでの部分の面積が0.495であるという条件がありますから、まさに正規分布表がもってこいの問題というわけですね。
正規分布表の見方ですが、例えば、0のところから1.84のところまでの面積が知りたいという場合は、$z_0$の縦軸が1.8、横軸が0.04のところが交わったところを見ます。それを見ると、表では0.4671とあるので、それが面積だということになります。このように、縦軸は小数第1位までの部分、横軸は小数第2位の部分を示しているわけです。
この表から0.495を探してみると、縦軸が2.5で横軸が0.07、つまり$z_0$が2.57のときは0.4949、縦軸が2.5で横軸が0.08、つまり$z_0$が2.58のときは0.4951となっていますから、この間と考えることができますが、選択肢のうち該当しそうなものは③の2.58しかありません。
(2)信頼区間のことが問題になっていますが、信頼区間の公式を確認しておきましょう。
母平均$m$の信頼区間は、標本の大きさを$n$、母標準偏差を$σ$とすると、
\( \displaystyle \overline{X}-u・\frac{σ}{\sqrt{n}}≦m≦\overline{X}+u・\frac{σ}{\sqrt{n}} \)
($u$は信頼区間のパーセント値から正規分布表を読み取った値)
$u$の値の読み取り方がポイントになりそうですが、その読み取り方は(1)の問題の方法と同じです。
たとえば、$L_1$を考えるために、信頼区間95%について考えるとしましょう。95% = 0.95ですが、これは、
\( P(-A≦Z≦A) = 0.95 \)
が成り立つときの$A$を考えるのと同じなんです。0.95の半分は0.475で、これを正規分布表から探すと、$z_0 = 1.96$のときの値だとわかります。この1.96が$u$の値だということになるわけです。
これより、信頼区間95%の幅は、
\( \displaystyle \overline{X}-1.96・\frac{σ}{\sqrt{n}}≦m≦\overline{X}+1.96・\frac{σ}{\sqrt{n}} \)
よって、$L_1$は、
$L_1$
\( \displaystyle = \overline{X}+1.96・\frac{σ}{\sqrt{n}}-\left(\overline{X}-1.96・\frac{σ}{\sqrt{n}}\right) \)
\( \displaystyle = 1.96・\frac{σ}{\sqrt{n}}+1.96・\frac{σ}{\sqrt{n}} \)
\( \displaystyle = 3.92・\frac{σ}{\sqrt{n}} \)
次に、$L_2$を考えましょう。これについては、信頼区間99%ですから、\( P(-A≦Z≦A) = 0.99 \)となる$A$の値を考えればいいのですが、それは(1)で求めたとおり2.58ですから、信頼区間99%の幅は、
\( \displaystyle \overline{X}-2.58・\frac{σ}{\sqrt{n}}≦m≦\overline{X}+2.58・\frac{σ}{\sqrt{n}} \)
よって、$L_2$は、
$L_2$
\( \displaystyle = \overline{X}+2.58・\frac{σ}{\sqrt{n}}-\left(\overline{X}-2.58・\frac{σ}{\sqrt{n}}\right) \)
\( \displaystyle = 2.58・\frac{σ}{\sqrt{n}}+2.58・\frac{σ}{\sqrt{n}} \)
\( \displaystyle = 5.16・\frac{σ}{\sqrt{n}} \)
よって、
\( \displaystyle \frac{L_2}{L_1} \)
\( \displaystyle = \frac{5.16・\displaystyle\frac{σ}{\sqrt{n}}}{3.92・\displaystyle\frac{σ}{\sqrt{n}}} \)
\( \displaystyle = \frac{5.16}{3.92} \fallingdotseq 1.3 \)
$L_3$について考えてみると、これは、信頼区間95%ですが、標本の大きさが$4n$ですから、
\( \displaystyle \overline{X}-1.96・\frac{σ}{\sqrt{4n}}≦m≦\overline{X}+1.96・\frac{σ}{\sqrt{4n}} \)
なので、$L_3$は、
$L_3$
\( \displaystyle = \overline{X}+1.96・\frac{σ}{\sqrt{4n}}-\left(\overline{X}-1.96・\frac{σ}{\sqrt{4n}}\right) \)
\( \displaystyle = 1.96・\frac{σ}{2\sqrt{n}}+1.96・\frac{σ}{2\sqrt{n}} \)
\( \displaystyle = 3.92・\frac{σ}{2\sqrt{n}} \)
\( \displaystyle = 1.96・\frac{σ}{\sqrt{n}} \)
よって、
\( \displaystyle \frac{L_3}{L_1} \)
\( \displaystyle = \frac{1.96・\displaystyle\frac{σ}{\sqrt{n}}}{3.92・\displaystyle\frac{σ}{\sqrt{n}}} \)
\( \displaystyle = \frac{1.96}{3.92} = 0.5 \)
答え.
タ ③
チ 1 ツ 3
テ 0 ト 5