この問題のポイント
y = axやy = logaxのグラフは1<aのときと0<a<1のときで形がちがう!
どこの点を必ず通るかや、対数のグラフは底を逆数にするとx軸に関して対称になることもチェック!
(1)重要な定理を確認しながら解きます。まず、\( 8^{\frac{5}{6}} \)についてですが、\( 8 = 2^3 \)ですね。8を何回もかけて計算するよりも、2を何回もかけて計算するほうが負担が少ないはずですから、そちらの計算をすることを考えましょう。
そうすると、\( 8^{\frac{5}{6}} \)は、
\( 8^{\frac{5}{6}} = (2^3)^{\frac{5}{6}} \)
とできます。そうすると、ここで指数関数についてのこんな法則が使えます。
\( (a^m)^n = a^{mn} \)
たとえば、\( (a^2)^3 \)ならば、
\( (a^2)^3 \)
\( = (a^2)×(a^2)×(a^2) \)
\( = a×a×a×a×a×a = a^6 \)
のようになるから、結局、\( a^{2×3} \)と同じということになりますね。
これを利用すると、
\( 8^{\frac{5}{6}} \)
\( = (2^3)^{\frac{5}{6}} \)
\( = 2^{\frac{5}{2}} \)
\( = \sqrt{2^5} \)
\( = \sqrt{32} = 4\sqrt{2} \)
次の対数の問題ですが、出てきている数字はみんな3を何乗かするとできる数字ばかりです。ということで、この公式を利用することを考えてみましょう。底の変換公式とよばれるものです。
\( \displaystyle \log_a b = \frac{\log_c b}{\log_c a} \)
つまり、分数の形にしたら、底を何の数にしてもいいっていうことですね。これを使って、底を3にすると、底の変換公式より、問題の式はこう変形できます。
\( \displaystyle \log_{27} \frac{1}{9} \)
\( \displaystyle = \frac{\log_3 \displaystyle\frac{1}{9}}{\log_3 {27}} \)
\( \displaystyle = \frac{\log_3 {9^{-1}}}{\log_3 {27}} \)
\( \displaystyle = \frac{\log_3 {3^{-2}}}{\log_3 {3^3}} \)
\( \displaystyle = \frac{-2}{3} \)
つまり、答えは\( \displaystyle -\frac{2}{3} \)です。
問題では、ウエとオをうめないといけませんから、ウエが-2、オが3ということになります。
(2)まず、指数関数と対数関数のグラフの形を確認しましょう。指数関数\( y = a^x \)のグラフはこのようになります。$a$がどのような数であっても、0乗は1ですから、グラフは必ず\( (0,1) \)を通るというのがポイントです。
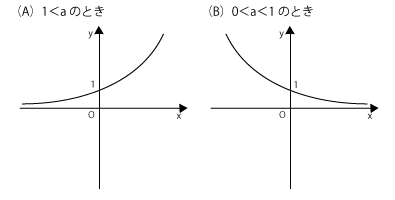
ふつうは、2乗、3乗、4乗、…としていけば、どんどん数は大きくなりますが、1より小さい数だと、どんどん数は小さくなりますね(たとえば、0.1だったら、0.01、0.001、0.0001、…となっていきます)。だから、グラフもこのような2パターンになるわけです。
対数関数\( y = \log_a x \)についても、同じように\( 1<a \)のときと\( 0<a<1 \)のときの2パターンに分けられます。対数関数のグラフについては、グラフは必ず\( (1,0) \)を通るというのがポイントです。
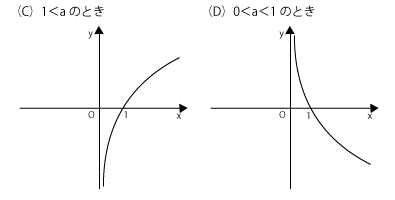
これをもとに、まずカに入るのが何かを考えると、どちらも指数関数で、片方は1より大きく、もう片方は1より小さい数ですから、上の図の(A)と(B)のグラフになりますから、左右逆にすると同じ形となります。$y$軸に関して対称の関係となります。
次に、キに入るものについてですが、片方が指数関数で、もう片方が対数関数のグラフとなっています。形としては、上の図の(A)と(C)のグラフになりますから、直線\( y = x \)に関して対称の関係となります。
クに入るものについて考えると、今度はどちらも対数関数で、片方は1より大きく、もう片方は1より小さい数ですから、上の図の(C)と(D)のグラフになります。上下逆さにすると同じ形になりますから、$x$軸に関して対称となります。
特に、\( y = \log_{2} x \)と\( \displaystyle y = \log_{\frac{1}{2}} x \)では、底が逆数どうしの関係になっていますね。このような、底が逆数どうしの対数関数は、グラフは$x$軸に関して対称になります。たとえば、今回の問題ならば、\( \displaystyle \log_{\frac{1}{2}} x \)を底の変換公式を使って、底を2にするよう変形させると、
\( \displaystyle \frac{\log_2 x}{\log_2 \displaystyle\frac{1}{2}} \)
\( \displaystyle = \frac{\log_2 x}{\log_2 {2^{-1}}} \)
\( \displaystyle = \frac{\log_2 x}{-1} \)
\( = -\log_2 x \)
つまり、\( \log_2 x \)と\( -\log_2 x \)というように、-1をかけた関係となるので、$x$軸に関して対称となるわけです。
最後に、ケに入るものを考えます。片方の対数関数は分数を使ってるんで、分数を使わない形に変形しましょう。すると、
\( \displaystyle y = \log_{2} {\frac{1}{x}} = \log_2 {x^{-1}} = -\log_2 x \)
ちなみに、\( \log_2 {x^{-1}} \)を\( -\log_2 x \)に変形したのは、次の定理を使っているからです。
\( \displaystyle \log_a {M^x} = x\log_a M \)
すると、\( y = \log_{2} x \)と\( y = -\log_{2} x \)のグラフということになりますので、さっきのクに入るものを考えたのと同じ状況になります。よって、この2つのグラフは$x$軸に関して対称となります。
答え.
ア 4 イ 2 ウエ -2 オ 3
カ ② キ ③ ク ① ケ ①