この問題のポイント
群数列は、各群の個数が何個でどんな数列になっているか、第n群までに数列全体で項数が何個かをつかもう!
階差数列の一般項の求め方もマスターしよう!
それぞれの群には、問題文に書いてあるとおり、$n$を使ってあらわすと$(3n-2)$個の項があります。
そして、数字を並べているだけなので、それぞれの群の数列は1ずつ増えている、つまり公差が1の等差数列だとわかりますね。
また、第1群から第$n$群までにある項数は全部で
\( \displaystyle 1+4+7+…+(3n-2) = \frac{1}{2}n(3n-1) \)…①です。
これを最初につかんでおくと、群数列は考えやすくなります。それでは、(1)から解いていきましょう。
(1)\( a_4 \)は、第4群の最後の項ですから、第1群から第4群までにある項数と等しいです。なので、①を使うと、
\( \displaystyle a_4 = \frac{1}{2}・4・(3・4-1) = \frac{1}{2}・4・11 = 22 \)
同じように考えると、\( a_n \)は、第1群から第$n$群までにある項数と等しく、\( a_{n-1} \)は、第1群から第$(n-1)$群までにある項数と等しいわけです。
第1群から第$n$群までにあるすべての項数のうち、第1群から第$(n-1)$群までにある項数を引いてしまったら、第$n$群にある項だけしか残らなくなります。
一番はじめにふれたとおり、第$n$群には項数は$(3n-2)$個あるはずですから、
\( a_n-a_{n-1} = 3n-2 \)…②となります。
この\( a_n-a_{n-1} \)という式は、ある項とその直前の項との差をあらわしています。これは階差数列をあらわしていることになりますね。ただし、階差数列というのは、本来は\( a_{n+1}-a_n \)であらわしますから、この式であらわしてみましょう。さっきの②を使うと、
\( a_{n+1}-a_n = 3(n+1)-2 = 3n+1 \)
階差数列を使って一般項を求めることができます(ただし\( n≧2 \)のとき)。次のような式で求めることができますね。
\( \displaystyle a_n = a_1+\sum_{k=1}^{n-1} (階差数列の一般項) \)
これを利用すると、
\( \displaystyle a_n = 1+\sum_{k=1}^{n-1} (3n+1) \)
\( \displaystyle = 1+3・\frac{1}{2}(n-1)n+(n-1) \)
\( \displaystyle = \frac{3}{2}n^2-\frac{1}{2}n \)
この式に\( n = 1 \)を代入しても答えが1となり、問題文にあった\( a_1 = 1 \)がきちんと成り立っています。このように、\( n = 1 \)のときもちゃんとこの式が成り立つかの確認はしなければいけません。
そして、600がどの群にあるかについてですが、600が第$n$群にあるとして、さっきの①を使って考えると、第$n$群までにある項数全部が600以上になればいいわけですから、この不等式を考えればいいということになります。
\( \displaystyle \frac{1}{2}n(3n-1)≧600 \)
これを解くと、
\( n(3n-1)≧1200 \)
\( 3n^2-n-1200≧0 \)
解の公式を使って解くと、こんなふうになります。
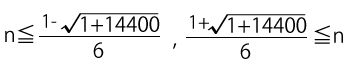
√の中が1+14400となり、解を出すととても大変になります。ただ、この問題では正確にこの不等式を解く必要性はありません(どこの群かがわかればいいので)。$n$がだいたいどれぐらいになりそうか見当をつけるだけにしましょう。
√の中身が14400だけだったら、\( 14400 = 120^2 \)ですから、√の部分は約120だとわかります。そして、$n$は第何群かを示しているわけですから、\( \displaystyle \frac{1+120}{6} \)より$n$は大きいとなります。
これより、$n$が21以上になれば項数全部が600以上になるということですから、600は第21群にあるということになります。
この第21群の中の何番目かを次に考えます。第20群の最後の項は、
\( \displaystyle a_{20} = \frac{3}{2}・20^2-\frac{1}{2}・20 = 600-10 = 590 \)
ということは、600は第21群の600-590 = 10番目ということになります。
(2)第$(n+1)$群の小さい方から$2n$番目ってことですから、言い換えれば第$n$群の最後、つまり\( a_n \)から$2n$個後の項ということですね?ということは、
\( b_n = a_n+2n \)
と表せます。
よって、
\( \displaystyle b_n = \frac{3}{2}n^2-\frac{1}{2}n+2n \)
\( \displaystyle = \frac{3}{2}n^2+\frac{3}{2}n \)
これは書き換えると、\( \displaystyle b_n = \frac{3n^2+3n}{2} \)ですから、
\( \displaystyle \frac{1}{b_n} = \frac{2}{3n^2+3n} \)
\( \displaystyle = \frac{2}{3n(n+1)} \)
\( \displaystyle = \frac{2}{3}・\frac{1}{n(n+1)} \)
そして、分母が因数分解されている形となっているこのような分数は、下の公式のような変形をすることができます。これを部分分数分解といいます。
\( \displaystyle \frac{1}{AB} = \frac{1}{B-A}\left(\frac{1}{A}-\frac{1}{B}\right) \)
今回は、$A$が$n$、$B$が$n+1$にあたると考えると\( B-A = 1 \)となりますから、( )の前の係数は考える必要はありません。よって、3分の2だけがついて
\( \displaystyle \frac{1}{b_n} = \frac{2}{3}\left(\frac{1}{n}-\frac{1}{n+1}\right) \)となります。
この部分分数分解をしておくと、この問題でも問われていますが、数列の和を求めるときに便利になります。今回の問題だとこうなるわけです。
\( \displaystyle \frac{2}{3}\left\{\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)\right.\ \)
\( \displaystyle \left.+…+\left(\frac{1}{n}-\frac{1}{n+1}\right)\right\} \)
この式で、マイナス2分の1とプラス2分の1、マイナス3分の1とプラス3分の1、マイナス4分の1とプラス4分の1、…と計算すると0になる組み合わせがいっぱいできます。その結果、次のようになります。
\( \displaystyle \frac{2}{3}\left(1-\frac{1}{n+1}\right) \)
\( \displaystyle = \frac{2}{3}\left(\frac{n+1}{n+1}-\frac{1}{n+1}\right) \)
\( \displaystyle = \frac{2}{3}・\frac{n}{n+1} \)
\( \displaystyle = \frac{2n}{3n+3} \)
答え.
アイ 22 ウ 3 エ 2
オ 3 カ 2 キ 2
ク 1 ケ 2
コサ 21 シス 10
セ 3 ソ 2 タ 2
チ 3 ツ 2
テ 2 ト 3 ナ 1
ニ 2 ヌ 3 ネ 3