この問題のポイント
点と直線の距離の公式を利用して方程式をたてよう!
(1)もし$l$が$y$軸と平行ならば、$l$の方程式は\( x = k \)とおくことができます。\( x = k \)のグラフと点$A$,$B$との関係は次の3パターンのうちのどれかになります。
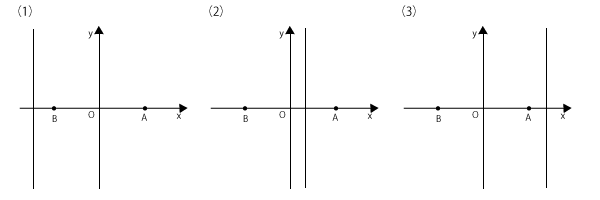
つまり、
(1)点$B$よりも左側にある場合
(2)点$A$と点$B$の間にある場合
(3)点$A$よりも右側にある場合
の3パターンです。
これはすなわち$k$を使って表すと、
(1)\( k≦-1 \)の場合
(2)\( -1<k<1 \)の場合
(3)\( 1≦k \)の場合
と考えることができます。
(1)の場合で考えてみると、
点$A$と$l$の距離は、\( 1-k \)
点$B$と$l$の距離は、\( -1-k \)
この和は\( 1-k+(-1-k) = -2k \)ですが、\( k≦-1 \)の場合、\( -2k≧2 \)となり、距離の和が1となることと矛盾します。
同様に、(2)の場合は、
点$A$と$l$の距離は、\( 1-k \)
点$B$と$l$の距離は、\( k-(-1) = k+1 \)
この和は\( 1-k+k+1 = 2 \)となり、これも距離の和が1となることと矛盾します。
(3)の場合は、
点$A$と$l$の距離は、\( k-1 \)
点$B$と$l$の距離は、\( k-(-1) = k+1 \)
この和は\( k-1+k+1 = 2k \)ですが、\( 1≦k \)の場合は\( 2k≧2 \)となり、距離の和が1となることと矛盾します。
以上から、(1)~(3)どの場合となっても、距離の和が1となることはないので、$l$が$y$軸と平行になることはありません。
解答のチェックポイント
- 直線$l$が$y$軸と平行だった場合の直線$l$の位置を場合分けして考えているか
- 場合分けしたそれぞれについて$k$の範囲を確認できているか
- 場合分けしたそれぞれについて、距離の和が2または2以上だということを示しているか
(2)$l$は$y$軸と平行ではありませんから、点\( (a,0) \)を通る傾き$m$である直線と考えられます。ちなみに、点\( (a,0) \)は線分$AB$と交わるんですから、\( -1≦a≦1 \)です。
点\( (p,q) \)を通り、傾き$t$の直線の方程式は、\( y-q = t(x-p) \)とおくことができます。
これを利用すると、点\( (a,0) \)を通る傾き$m$である直線は、\( y = m(x-a) \)とおけます。これは、
\( y = mx-ma \)
\( mx-y-ma = 0 \)とおけます。
この直線と点$A$,$B$の距離を考えていけばいいわけですが、点と直線の距離は公式で求めることができましたね?
すなわち、点\( (p,q) \)と直線\( ax+by+c = 0 \)の距離は、
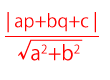
この公式を利用します。つまり、\( A(1,0) \)と$l$の距離と\( B(-1,0) \)と$l$の距離の和が1なので、
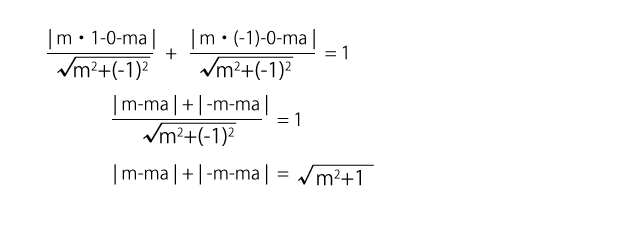
この式の両辺を2乗すると、
\begin{eqnarray} &&\small{(m-ma)^2+(-m-ma)^2+2|(m-ma)(-m-ma)|}\\ &&\small{~~~~= m^2+1}\\ &&\small{m^2(1-a)^2+m^2(1+a)^2+2|m^2(1-a)(1+a)|}\\ &&\small{~~~~= m^2+1}\\ &&\small{m^2(1-2a+a^2)+m^2(1+2a+a^2)+2|m^2(1-a^2)|}\\ &&\small{~~~~= m^2+1}\\ &&\small{2m^2(1+a^2)+2m^2|1-a^2| = m^2+1…①}\\ \end{eqnarray}
ここで、$a$の範囲は\( -1≦a≦1 \)ですので、\( 1-a^2≧0 \)です。ということは、絶対値の符号をはずすときは-をつける必要はないので、
\begin{eqnarray} &&\small{2m^2(1+a^2)+2m^2(1-a^2) = m^2+1}\\ &&\small{2m^2+2m^2a^2+2m^2-2m^2a^2 = m^2+1}\\ &&\small{4m^2 = m^2+1}\\ &&\small{3m^2 = 1}\\ &&\small{m^2 = \frac{1}{3}}\\ \end{eqnarray}
よって、\( \displaystyle m = ±\frac{1}{\sqrt{3}} = ±\frac{\sqrt{3}}{3} \)
これより、$l$の傾きは\( \displaystyle ±\frac{\sqrt{3}}{3} \)です。
(3)直線$l$は(2)と同じように、\( mx-y-ma = 0 \)とおくことができます。ただし、(3)では$l$は線分$AB$と交わらないので、$a$の範囲は\( a<-1 \),\( 1<a \)です。
この直線と原点(0,0)の距離は、さっきの点と直線の距離の公式を使うとこのような式となります。
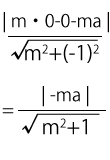
絶対値の記号や根号があると計算がしにくいので、2乗します。$l$と原点の距離を$d$とすると、
\( \displaystyle d^2 = \frac{m^2a^2}{m^2+1} \)
$d$については、これ以上計算ができませんので、ここでいったん「$A$と$l$の距離と$B$と$l$の距離の和が1」という条件に立ち返りましょう。これについては(2)と同じように計算できるわけですから、そのやり方で計算すれば①の式が得られます。
そしてここでは、$a$の範囲は\( a<-1 \),\( 1<a \)なんですから、\( 1-a^2<0 \)です。よって、ここでは、絶対値の符号をはずすときは-をつける必要がありますから、
\( 2m^2(1+a^2)-2m^2(1-a^2) = m^2+1 \)
\( 2m^2+2m^2a^2-2m^2+2m^2a^2 = m^2+1 \)
\( 4m^2a^2 = m^2+1 \)
これをさっきの$d^2$の式に代入すると、
\( \displaystyle d^2 = \frac{m^2a^2}{4m^2a^2} = \frac{1}{4} \)
\( d>0 \)ですから、\( \displaystyle d = \frac{1}{2} \)
これで、$l$と原点との距離が求まりました。
答え.
(1)
(上にて説明)
(2)
\( \displaystyle ±\frac{\sqrt{3}}{3} \)
(3)
\( \displaystyle \frac{1}{2} \)