この問題のポイント
ベクトルの内積、平行・垂直に関する公式をマスターしよう!
a→・b→ = |a→||b→|cosθ
a→//b→ならば、a→ はb→の実数倍
a→⊥b→ならば内積は0
(1)まず、\( \vec{a}-\vec{b} \)と\( \vec{c} \)が平行であることを手がかりに考えましょう。\( \vec{a}-\vec{b} \)のように、ベクトルの計算式がありますが、この問題では、ベクトルの成分が与えられています。成分が与えられている場合は、$x$成分どうし、$y$成分どうしで計算します。よって、
\( \vec{a}-\vec{b} \)
\( = (p-(-1),2-3) \)
\( = (p+1,-1) \)
そして、\( \vec{a}-\vec{b} \)と\( \vec{c} \)は平行なんですから、\( \vec{a}-\vec{b} \)は\( \vec{c} \)の実数倍になります。つまり、
\( \vec{a}-\vec{b} = k\vec{c} \)
と表せます。
これより、
\( (p+1,-1) = k(1,q) \)
$x$成分どうし、$y$成分どうしで計算すればいいので、
\( p+1 = k \) …①
\( -1 = qk \) …②
①より、\( p = k-1 \) …③
②より、\( \displaystyle q = -\frac{1}{k} \) …④
これ以上は計算できないので、ここで次に、\( \vec{b}-\vec{c} \)と\( \vec{a} \)が垂直であることを手がかりに考えていきましょう。さっきと同じように計算すれば、
\( \vec{b}-\vec{c} \)
\( = (-1-1,3-q) \)
\( = (-2,3-q) \)
\( \vec{b}-\vec{c} \)と\( \vec{a} \)は垂直ですから、\( \vec{b}-\vec{c} \)と\( \vec{a} \)の内積は0です。\( \vec{b}-\vec{c} \)と\( \vec{a} \)のかけ算も$x$成分どうし、$y$成分どうしでかけ算してそれをたせばOKです。なので、
\( -2p+2(3-q) = 0 \)
この式に③と④を代入して
\( \displaystyle -2(k-1)+2(3+\frac{1}{k}) = 0 \)
\( \displaystyle -2k+2+6+\frac{2}{k} = 0 \)
\( \displaystyle -2k+8+\frac{2}{k} = 0 \)
両辺にkをかけて、
\( -2k^2+8k+2 = 0 \)
両辺を-2でわって、
\( k^2-4k-1 = 0 \)
解の公式を使って解くと、\( k = 2±\sqrt{5} \)
\( k = 2+\sqrt{5} \)と\( k = 2-\sqrt{5} \)をそれぞれ③に代入してまとめると、
\( p = 1±\sqrt{5} \)
$q$については、\( k = 2+\sqrt{5} \)(\( p = 1+\sqrt{5} \)のときの$k$の値)を④に代入すると、
\( \displaystyle q = -\frac{1}{2+\sqrt{5}} \)
\( \displaystyle = -\frac{2-\sqrt{5}}{(2+\sqrt{5})(2-\sqrt{5})} \)
\( \displaystyle = -\frac{2-\sqrt{5}}{4-5} \)
\( \displaystyle = -\frac{2-\sqrt{5}}{-1} \)
\( = 2-\sqrt{5} \)
\( k = 2-\sqrt{5} \)(\( p = 1-\sqrt{5} \)のときの$k$の値)を④に代入したら、
\( \displaystyle q = -\frac{1}{2-\sqrt{5}} \)
\( \displaystyle = -\frac{2+\sqrt{5}}{(2-\sqrt{5})(2+\sqrt{5})} \)
\( \displaystyle = -\frac{2+\sqrt{5}}{4-5} \)
\( \displaystyle = -\frac{2+\sqrt{5}}{-1} \)
\( = 2+\sqrt{5} \)
すなわち、\( p = 1+\sqrt{5} \)のときは\( q = 2-\sqrt{5} \)、\( p = 1-\sqrt{5} \)のときは\( q = 2+\sqrt{5} \)です。
(2)まず、\( \sqrt{2}|\vec{a}| = |\vec{b}| \)を手がかりに考えます。この式の両辺を2乗すると、
\( 2|\vec{a}|^2 = |\vec{b}|^2 \)
ベクトルの絶対値の2乗は、($x$成分の2乗)+($y$成分の2乗)に等しいので、
\( |\vec{a}|^2 = p^2+2^2 = p^2+4 \)
\( |\vec{b}|^2 = (-1)^2+3^2 = 10 \)
よって、
\( 2(p^2+4) = 10 \)
\( 2p^2+8 = 10 \)
\( 2p^2 = 2 \)
\( p^2 = 1 \)
\( p = ±1 \)
これで$p$の値が求まりました。$q$の値は、\( \vec{a}-\vec{b} \)と\( \vec{c} \)のなす角が60°というのを手がかりに考えましょう。
[1] \( p = 1 \)のとき
このときの\( \vec{a}-\vec{b} \)は、
\( \vec{a}-\vec{b} \)
\( = (1-(-1),2-3) \)
\( = (2,-1) \)
これと\( \vec{c} = (1,q) \)とのなす角が60°です。
\( \displaystyle \cos 60° = \frac{1}{2} \)ですね?
これと内積の公式を使って、
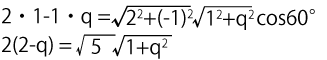
両辺を2乗して、
\( 5(1+q^2) = \{2(2-q)\}^2 \)
\( 5+5q^2 = (4-2q)^2 \)
\( 5+5q^2 = 16-16q+4q^2 \)
\( q^2+16q-11 = 0 \)
これを解の公式を使って解くと、
\( q = -8±\sqrt{75} \)
つまり、\( q = -8±5\sqrt{3} \)
[2] \( p = -1 \)のとき
このときの\( \vec{a}-\vec{b} \)は、
\( \vec{a}-\vec{b} \)
\( = (-1-(-1),2-3) \)
\( = (0,-1) \)
さっきと同じように考えれば、
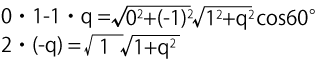
この式に注意すべきことがあります。この式の右辺、つまり=の右側は√どうしのかけ算なので、必ず正の数になるはずです。ということは、左辺も正の数になるはずです。ということは、
\( -q>0 \)
\( q<0 \)の数にならないといけませんね。
それを確認したところで、[1]と同じように両辺を2乗すると、
\( 1+q^2 = (-2q)^2 \)
\( 1+q^2 = 4q^2 \)
\( 3q^2 = 1 \)
\( \displaystyle q^2 = \frac{1}{3} \)
\( \displaystyle q = ±\frac{\sqrt{3}}{3} \)
ただし、さきほど確認したとおり、\( q<0 \)でないといけないんですから、
\( \displaystyle q = -\frac{\sqrt{3}}{3} \)
答え.
(1)
\( (p,q) = (1+\sqrt{5},2-\sqrt{5}),(1-\sqrt{5},2+\sqrt{5}) \)
(2)
\( \displaystyle (p,q) = (1,-8±5\sqrt{3}),(-1,-\frac{\sqrt{3}}{3}) \)