問題ページにもどる

この問題のポイント

まず、領域$D$がどの領域なのかがわからないと、この問題は解けませんから、領域の図をかくことから始めましょう。

境界線となるグラフは、
\( x^2+y^2 = 1 \)（＝中心が原点で半径1の円）
\( x^2+y^2 = 4 \)（＝中心が原点で半径2の円）
\( y = \sqrt{3}x \)
\( y = 0 \)（＝x軸）

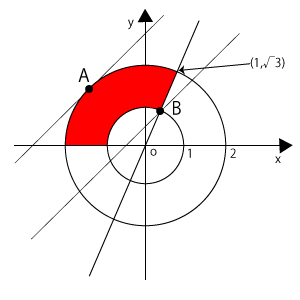
そして、それぞれのグラフを書いて、該当する範囲を赤くぬりつぶすと、右図のようになります。よって、領域$D$は右図の赤色部分です。もちろん、不等号に「＝」があったので、境界線も含みますね。

さて、領域が求まったので、いよいよ $y$-$x$ について考えましょう。

とりあえず、「$y$-$x$ の最大値、最小値」と言ってるのですから、この式は何らかの値になるはずです。なので、
\( y-x = k \)
とおきましょう。

そして、領域を考えるときに座標平面を書きました。こういう座標平面でグラフを書くときに、よく、「$y$ = …」という形にしますね。この式もそうしてみましょう。

すると、
\( y = x+k \) …①
となり、$k$は、直線①のy切片だということがわかります。

ということは、直線①が領域$D$を通るときのy切片が最大になるときが、$y$-$x$ の最大値となりますね。
では、どのときがy切片が最大となるでしょう。直線①を動かして考えましょう。

ちょうど、右上の図の細い直線が直線①となりますが、この直線が円\( x^2+y^2 = 4 \)と、図の点Aで接しているときが、y切片が最大となりますね。

接しているということは、円の方程式と直線の方程式の連立方程式は解が1つだけになるはずです。

\( y = x+k \) を\( x^2+y^2 = 4 \)に代入して、
\( x^2+{x+k}^2 = 4 \)
\( x^2+x^2+2kx+k^2 = 4 \)
\( 2x^2+2kx+k^2-4 = 0 \)

この方程式の（判別式）=0 となればいいはずです。

\(\frac{D}{4} = k^2-2・(k^2-4) = 0\)
\( k^2-2k^2+8 = 0 \)
\( -k^2 = -8 \)
\( k^2 = 8 \)
\( k = ±2\sqrt{2} \)

直線①は、円\( x^2+y^2 = 4 \)と第2象限で接しているのですから、図より考えて、$k$＞0
よって、\( k = 2\sqrt{2} \)
これが、最大値となります。

y切片が最小となるのは、どんなときかというと、直線①が点Bを通るときですね。
点Bの座標は、\( x^2+y^2 = 1 \)と\( y = \sqrt{3}x \)の交点なのですから、その連立方程式を解いて求まります。求めると、(\(\displaystyle \frac{1}{2}，\frac{\sqrt{3}}{2}\))とわかります。

この座標を、直線①の方程式に代入して
\( \displaystyle \frac{\sqrt{3}}{2} = \frac{1}{2}+k \)
\( \displaystyle k = \frac{\sqrt{3}}{2}-\frac{1}{2} \)

解答には、(√3-1)/2と書けばOKです。

答え．
最大値　\(2\sqrt{2}\)
最小値　\( \displaystyle \frac{\sqrt{3}}{2}-\frac{1}{2} \)