この問題のポイント
円に内接する四角形で対角の和は180°
→1つの角でcosθ、sinθとするとその対角の三角比は-cosθ、sinθ!
(1)$AB$の長さを$x$とおくと、\( \displaystyle x = \frac{CD}{3} \)なので\( CD = 3x \)
\( \displaystyle x^2 = \frac{BC}{2} \)なので\( BC = 2x^2 \)
\( \displaystyle x^2 = \frac{DA}{4} \)なので\( DA = 4x^2 \)
ここで、四角形$ABCD$は円に内接するので対角(向かい合っている角)の和は180°です。\( \displaystyle \cos∠BAD = -\frac{1}{2} \)なので、$∠BAD$の大きさは120°です。ということは、$∠BCD$は60°ということになります。
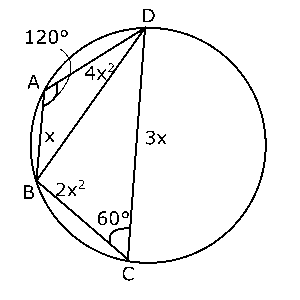
長さや角度がわかっている部分を書き込むと右の図のようになりますが、この四角形は$BD$で2つの三角形に分けることができます。
$△BAD$において、余弦定理を使うとこのようになります。
\( BD^2 = AB^2+AD^2-2・AB・AD・\cos∠BAD \)
\( \displaystyle BD^2 = x^2+(4x^2)^2-2・x・4x^2・\left(-\frac{1}{2}\right) \)
\( BD^2 = 16x^4+4x^3+x^2 \)…[1]
$△BCD$において、余弦定理を使うと
\( BD^2 = BC^2+DC^2-2・BC・DC・\cos∠BCD \)
\( \displaystyle BD^2 = (2x^2)^2+(3x)^2-2・2x^2・3x・\frac{1}{2} \)
\( BD^2 = 4x^4-6x^3+9x^2 \)…[2]
[1],[2]より、\( 16x^4+4x^3+x^2 = 4x^4-6x^3+9x^2 \)
\( x \neq 0 \)より、両辺を$x^2$で割って\( 16x^2+4x+1 = 4x^2-6x+9 \)
\( 12x^2+10x-8 = 0 \)
両辺を2で割って\( 6x^2+5x-4 = 0 \)
\( (2x-1)(3x+4) = 0 \)
\( \displaystyle x = \frac{1}{2},-\frac{4}{3} \)
$x$は$AB$の長さのことでしたから、負の数は不適なので\( \displaystyle x = \frac{1}{2} \)です。
これを[1]に代入すると、
\( \displaystyle BD^2 = 16・\left(\frac{1}{2}\right)^4+4・\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2 \)
\( \displaystyle = 16・\frac{1}{16}+4・\frac{1}{8}+\frac{1}{4} \)
\( \displaystyle = 1+\frac{1}{2}+\frac{1}{4} \)
\( \displaystyle = \frac{7}{4} \)
$BD>0$なので\( \displaystyle BD = \frac{\sqrt{7}}{2} \)
これで$BD$の長さが求まりましたが、ちょうど$BD$に向かい合った角である$∠BAD$の角度もわかっており、しかも$△BAD$は四角形$ABCD$の一部なんですから半径$r$の円に内接しています。ということは、正弦定理を使うことができますね?
$∠BAD$の大きさは120°なので\( \displaystyle \sin∠BAD = \frac{\sqrt{3}}{2} \)より、正弦定理を使うと、
\( \displaystyle \frac{BD}{\sin∠BAD} = 2r \)
\( \displaystyle 2r = \frac{\sqrt{7}}{2}÷\frac{\sqrt{3}}{2} \)
\( \displaystyle ∴2r = \frac{\sqrt{7}}{2}×\frac{2}{\sqrt{3}} = \frac{\sqrt{7}}{\sqrt{3}} \)
\( \displaystyle ∴r = \frac{\sqrt{7}}{2\sqrt{3}} \)
\( \displaystyle = \frac{\sqrt{7}・\sqrt{3}}{2\sqrt{3}・\sqrt{3}} \)
\( \displaystyle = \frac{\sqrt{7}・\sqrt{3}}{2・3} \)
\( \displaystyle = \frac{\sqrt{21}}{6} \)
(2)① 〈指針〉
$∠BAD = θ$とおくと、四角形$ABCD$は円に内接しているので、それに向かい合った角である$∠BCD$は$180°-θ$とおけます。すると、\( \cos∠BAD \),\( \sin∠BAD \)は\( \cosθ \),\( \sinθ \)とすることができ、\( \cos∠BCD \),\( \sin∠BCD \)は
\( \cos∠BCD = \cos(180°-θ) = -\cosθ \)
\( \sin∠BCD = \sin(180°-θ) = \sinθ \)とおけます。
このように、1つの角を$θ$とおくと、向かい合った角も$θ$であらわすことができ、しかもその2つの角について\( \cos \),\( \sin \)が使いやすくなります。
さらに、さっきの(1)のように、四角形$ABCD$を2つの三角形に分ければ、(1)のときと同じように共通する辺について2通りの式であらわすことができます。これを使って、\( \cos∠BAD \)を$x$を使った式にするとどうなるかを考えるといいでしょう。
〈証明〉
$∠BAD = θ$とする。$△ABD$において、余弦定理を使うと
\( BD^2 = AB^2+AD^2-2・AB・AD・\cos∠BAD \)
\( = 6^2+(5-x)^2-2・6・(5-x)\cosθ \)
\( = 36+25-10x+x^2-12(5-x)\cosθ \)
\( = x^2-10x+61-12(5-x)\cosθ \)…[3]
$△BCD$において、余弦定理を使うと
\( BD^2 = BC^2+CD^2-2・BC・CD・\cos∠BCD \)
\( = 3^2+x^2-2・3・x・\cos(180°-θ) \)
\( = 9+x^2-6x・(-\cosθ) \)
\( = x^2+9+6x\cosθ \)…[4]
[3],[4]より、
\begin{eqnarray} &&x^2-10x+61-12(5-x)\cosθ = x^2+9+6x\cosθ\\ &&x^2-x^2-10x+61-9 = 12(5-x)\cosθ+6x\cosθ\\ &&\{12(5-x)+6x\}\cosθ = 52-10x\\ &&(60-6x)\cosθ = 52-10x\\ &&\cosθ = \frac{52-10x}{60-6x} = \frac{26-5x}{30-3x} = \frac{26-5x}{3(10-x)} \end{eqnarray}
よって、\( \displaystyle \cos∠BAD = \frac{26-5x}{3(10-x)} \)である。
② 四角形$ABCD$の面積を直接求めることはできませんから、$△ABD$と$△BCD$に分けてそれぞれの面積を考えていきましょう。
三角形の2辺の長さが$a$,$b$でその間の角が$θ$とすると、面積は\( \displaystyle \frac{1}{2}\sinθ \)で求まりますから、\( \sin∠BAD \)を求めます。
①より、\( \displaystyle \cos∠BAD = \frac{26-5x}{3(10-x)} \)と求めています。そして、$0°<∠BAD<180°$なので\( \sin∠BAD>0 \)です。よって、
\begin{eqnarray} &&\sin∠BAD\\ &&= \sqrt{1-\cos^2∠BAD}\\ &&= \sqrt{1-\left\{\frac{26-5x}{3(10-x)}\right\}^2}\\ &&= \sqrt{1-\frac{(26-5x)^2}{\{3(10-x)\}^2}}\\ &&= \sqrt{\frac{\{3(10-x)\}^2-(26-5x)^2}{\{3(10-x)\}^2}}\\ &&= \sqrt{\frac{9(10-x)^2-(26-5x)^2}{\{3(10-x)\}^2}}\\ &&= \sqrt{\frac{9(100-20x+x^2)-(676-260x+25x^2)}{\{3(10-x)\}^2}}\\ &&= \sqrt{\frac{-16x^2+80x+224}{\{3(10-x)\}^2}}\\ &&= \sqrt{\frac{16(-x^2+5x+14)}{\{3(10-x)\}^2}}\\ &&= \frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \end{eqnarray}
よって、$△ABD$の面積は、
\( \displaystyle \frac{1}{2}・AB・AD・\sin∠BAD \)
\( \displaystyle = \frac{1}{2}・6・(5-x)・\sin∠BAD \)
\( \displaystyle = 3(5-x)・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \)
$△BCD$の面積は、
\( \displaystyle \frac{1}{2}・BC・CD・\sin∠BCD \)
\( \displaystyle = \frac{1}{2}・3・x・\sin∠BCD \)
\( \displaystyle = \frac{3}{2}x・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \)
これより、
$S(x)$
$= △ABD+△BCD$
\( \displaystyle = 3(5-x)・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)}+\frac{3}{2}x・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \)
\( \displaystyle = (15-\frac{3}{2}x)・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \)
\( \displaystyle = \frac{3}{2}(10-x)・\frac{4\sqrt{-x^2+5x+14}}{3(10-x)} \)
\( = 2\sqrt{-x^2+5x+14} \)
この式を見ると、ルートの中は2次関数になっています。これを平方完成すると、
\( S(x) = 2\sqrt{-x^2+5x+14} \)
\( = 2\sqrt{-(x^2-5x)+14} \)
\( \displaystyle = 2\sqrt{-\left(x^2-5x+\frac{25}{4}-\frac{25}{4}\right)+14} \)
\( \displaystyle = 2\sqrt{-\left(x^2-5x+\frac{25}{4}\right)+\frac{25}{4}+14} \)
\( \displaystyle = 2\sqrt{-\left(x-\frac{5}{2}\right)^2+\frac{81}{4}} \)
これより、$S(x)$は\( \displaystyle x = \frac{5}{2} \)のときに最大値をとります。その最大値は、
\( \displaystyle 2\sqrt{\frac{81}{4}} = 2・\frac{9}{2} = 9 \)
(3)$AB = x$,$DA = y$とします。四角形の周の長さが44で、辺$BC$と辺$CD$の長さがいずれも13なので、
\( x+y+13+13 = 44 \)
\( x+y = 44-26 = 18 \)…[5]
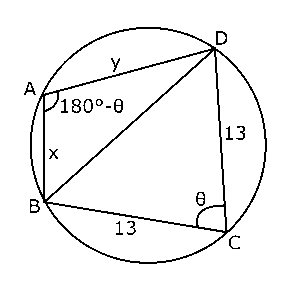
ここで、右の図のように$∠BCD = θ$とおきます。四角形$ABCD$は円に内接しているんですから、$∠BAD = 180°-θ$とおけます。さっきの(1)や(2)と同じように2つの三角形に分けて考えましょう。$BD$をひくと、$△BCD$において、余弦定理より、
\( BD^2 = BC^2+CD^2-2・BC・CD・\cos∠BCD \)
\( = 13^2+13^2-2・13・13・\cosθ \)
\( = 169+169-2・169・\cosθ \)
\( = 338-338\cosθ \)…[6]
$△BAD$において、余弦定理より、
\( BD^2 = AB^2+AD^2-2・AB・AD・\cos∠BAD \)
\( = x^2+y^2-2xy・\cos(180°-θ) \)
\( = x^2+y^2-2xy・(-\cosθ) \)
\( = x^2+y^2+2xy\cosθ \)…[7]
さらに、四角形$ABCD$は半径\( \displaystyle \frac{65}{8} \)の円に内接していますから、さっきの(1)のように正弦定理を使うことができます。
\( \displaystyle \frac{BD}{\sinθ} = 2×\frac{65}{8} \)が成り立つので、
\( \displaystyle BD = \frac{65}{4}\sinθ \)
これを[6]に代入すると、
\( \displaystyle \left(\frac{65}{4}\sinθ\right)^2 = 338-338\cosθ \)
\( \displaystyle \frac{65^2}{16}\sin^2θ = 338-338\cosθ \)
\( \displaystyle \frac{5^2×13^2}{16}(1-\cos^2θ) = 338(1-\cosθ) \)
\( \displaystyle \frac{5^2×13^2}{16}(1-\cos^2θ) = 2×13^2(1-\cosθ) \)
\( \displaystyle \frac{25}{16}(1-\cos^2θ) = 2(1-\cosθ) \)
\( 25(1-\cos^2θ) = 32(1-\cosθ) \)
\( 25(1+\cosθ)(1-\cosθ) = 32(1-\cosθ) \)
\( \cosθ \neq 1 \)より($θ$が0°や180°だと四角形ができないので)、\( 1-\cosθ \neq 0 \)なので、
\( 25(1+\cosθ) = 32 \)
\( \displaystyle 1+\cosθ = \frac{32}{25} \)
\( \displaystyle \cosθ = \frac{7}{25} \)
これを[6]に代入すると、
\( \displaystyle BD^2 = 338-338・\frac{7}{25} \)
\( \displaystyle = 338\left(1-\frac{7}{25}\right) \)
\( \displaystyle = 338・\frac{18}{25} \)
\( \displaystyle = 2・13^2・\frac{2・3^2}{5^2} \)
\( \displaystyle = \frac{2^2・13^2・3^2}{5^2} \)
よって、\( \displaystyle BD = \frac{2・13・3}{5} = \frac{78}{5} \)
これと\( \cosθ \)の値を[7]に代入すると、
\( \displaystyle \left(\frac{78}{5}\right)^2 = x^2+y^2+2xy・\frac{7}{25} \)
\( \displaystyle \frac{78^2}{25} = (x+y)^2-2xy+2xy・\frac{7}{25}xy \)
\( \displaystyle \frac{78^2}{25} = (x+y)^2-2xy+\frac{14}{25}xy \)
[5]より、\( \displaystyle \frac{78^2}{25} = 18^2-2xy+\frac{14}{25}xy \)
\( 78^2 = 5^2・18^2-50xy+14xy \)
\( 50xy-14xy = (18・5)^2-78^2 \)
\( 50xy-14xy = 90^2-78^2 \)
\( 36xy = (90+78)(90-78) \)
\( \displaystyle xy = \frac{168×12}{36} = 56 \)…[8]
[5]より、\( y = 18-x \)であり、これを[8]に代入すると、
\( x(18-x) = 56 \)
\( 18x-x^2 = 56 \)
\( x^2-18x+56 = 0 \)
\( (x-4)(x-14) = 0 \)
\( ∴x = 4,14 \)
\( y = 18-x \)なので、\( x = 4 \)のとき\( y = 14 \)
\( x = 14 \)のとき\( y = 4 \)
よって、$AB$ = 4,$DA$ = 14または$AB$ = 14,$DA$ = 4です。
答え.
(1)
(ア) …\( \displaystyle \frac{1}{2} \) (イ) …\( \displaystyle = \frac{\sqrt{21}}{6} \)
(2)
① (上の〈証明〉参照)
② \( \displaystyle x = \frac{5}{2} \)のとき最大値9
(3)
$AB$ = 4,$DA$ = 14または$AB$ = 14,$DA$ = 4