この問題のポイント
正八面体は合同な正四角錐が2つ、または合同な三角錐が8つ集まった立体!
立体図形での最短距離は展開図にして考える!
1辺の長さが6の正三角形の面積について、正三角形の1つの角は60°なので、
\( \displaystyle \frac{1}{2}・6・6・\sin60° \)
\( \displaystyle = \frac{1}{2}・6・6・\frac{\sqrt{3}}{2} = 9\sqrt{3} \)
正八面体ですから、この正三角形が8つあるということなので、正八面体の表面積は、
\( 9\sqrt{3}・8 = 72\sqrt{3} \)です。
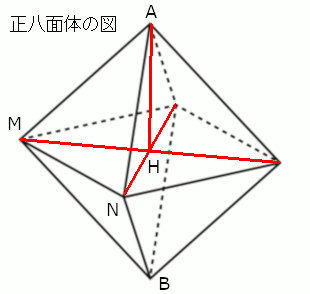
正八面体は、合同な(形がまったく同じの)正四角錐2つについて、底面の正方形どうしをくっつけたときと同じ立体図形になっています。ですから、正八面体の体積については、その正四角錐の体積を考えていくといいですね。
正四角錐の底面は1辺の長さが6の正方形です。高さについては、右の図のように記号をうつとして、$AM$の長さは正八面体の1辺なので6です。$MH$は1辺の長さが6の正方形の対角線の半分です。対角線の長さは\( 6\sqrt{2} \)ですから、\( MH = 3\sqrt{2} \)です。
よって、三平方の定理より、
\( AH^2+MH^2 = AM^2 \)
\( AH^2+(3\sqrt{2})^2 = 6^2 \)
\( AH^2+18 = 36 \)
\( AH^2 = 18 \)より、\( AH = 3\sqrt{2} \)です。
これが正四角錐の高さとなりますから、正四角錐の体積は\( \displaystyle 6・6・3\sqrt{2}・\frac{1}{3} = 36\sqrt{2} \)
これが2つくっついた形と同じなので、正八面体の体積は\( 36\sqrt{2}・2 = 72\sqrt{2} \)です。
次に、すべての面に接する球について考えます。その球の中心を$O$とします。さっきの「正八面体の図」を使って考えると、$△AMN$を底面にして頂点を$O$にした三角錐ができます。これと同じような三角錐をほかの7つの面についても考えることができますね?
ということは、それぞれの面の三角形が底面、球の中心が頂点である、合同な小さい三角錐8つが合わさって正八面体が完成していると考えることができます。この三角錐の高さを$r$とおくと、ちょうどそれが球の半径と同じになります。
さらに、1辺の長さが6の正三角形の面積は\( 9\sqrt{3} \)と求めていましたから、この三角錐の体積は、
\( \displaystyle 9\sqrt{3}・r・\frac{1}{3} = 3\sqrt{3}r \)とおけます。
正八面体の体積は\( 72\sqrt{2} \)と求めていました。三角錐8つが合わさって正八面体になるので、
\( 3\sqrt{3}r・8 = 72\sqrt{2} \)
\( \sqrt{3}r = 3\sqrt{2} \)
\( \displaystyle r = \frac{3\sqrt{2}}{\sqrt{3}} = \frac{3\sqrt{6}}{3} = \sqrt{6} \)
これで球の半径が求まりました。この球の表面積は公式を使って求めると、
\( 4π・(\sqrt{6})^2 = 24π \)
$A$,$B$間の距離は、さっきの「正八面体の図」を使って考えると、$A$から折れ曲がることなくまっすぐ$B$まで下りる直線の長さと等しいです。つまり、$AH+BH$、正四角錐の高さの2倍に等しいです。正四角錐の高さは\( 3\sqrt{2} \)と求まっていますから、$A$,$B$間の距離は\( 6\sqrt{2} \)です。
$AC+BC$が最小となるときについてですが、これは言い換えれば、$A$から正八面体の面の上を通りながら$C$を通過して$B$まで行ける最短ということになります。空間図形のこのような問題では、関係する面の展開図を描いて考えると解きやすいことが多いです。
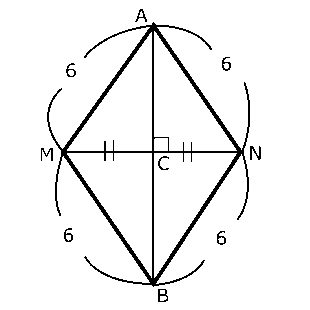
さっきの「正八面体の図」を使って考えると、$MN$上に$C$をおいたとすると、$△AMN$と$△BMN$の展開図が右の図のように描けます。この展開図からわかるとおり、$C$が$MN$の中点にあれば、$A$,$B$,$C$が一直線上に並ぶので$AC+BC$は最小になります。
$AM$は正三角形の1辺なので、長さは6です。そして、$C$は正三角形の1辺の中点だから、$CM$の長さは3です。これより、\( AC = 3\sqrt{3} \)です。同様に考えれば\( BC = 3\sqrt{3} \)です。
$A$から正八面体の面の上を通らないでまっすぐ$B$まで下りたときの長さは、さっき求めたとおり\( 6\sqrt{2} \)です。$△ABC$について、余弦定理を使うと\( \cos∠ACB \)はこのように求まります。
\( \displaystyle \cos∠ACB = \frac{AC^2+BC^2-AB^2}{2・AC・BC} \)
\( \displaystyle = \frac{(3\sqrt{3})^2+(3\sqrt{3})^2-(6\sqrt{2})^2}{2・3\sqrt{3}・3\sqrt{3}} \)
\( \displaystyle = \frac{27+27-72}{54} \)
\( \displaystyle = -\frac{18}{54} = -\frac{1}{3} \)
答え.
ア…\( 72\sqrt{3} \)
イ…\( 72\sqrt{2} \)
ウ…\( \sqrt{6} \)
エ…\( 24π \)
オ…\( 6\sqrt{2} \)
カ…\( \displaystyle -\frac{1}{3} \)