この問題のポイント
円と2直線が交わった図で線分の長さを求めるときや、円に関する線分のかけ算の証明、4点が同じ円の周上にあることの証明では方べきの定理が使えることがある!
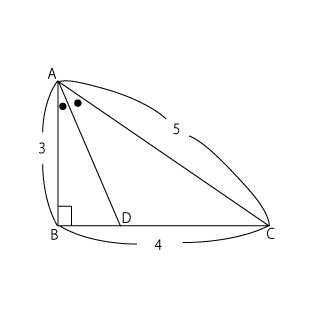
\( 3^2+4^2 = 5^2 \)、つまり\( AB^2+BC^2 = CA^2 \)が成り立つので、$△ABC$は$∠B$が90°の直角三角形です。そして、右の図のように、$AD$は$∠BAC$の二等分線ですから、角の二等分線の性質より、
\( AB:AC = BD:DC \)
\( AB:AC = 3:5 \)ですから、$BD$の長さは辺$BC$の\( \displaystyle \frac{3}{3+5} \)、つまり\( \displaystyle \frac{3}{8} \)です。よって、
\( \displaystyle BD = 4×\frac{3}{8} = \frac{3}{2} \)
そして、$∠B$が90°なので$△ABD$において三平方の定理より、\( AB^2+BD^2 = AD^2 \)
\( \displaystyle ∴AD^2 = 3^2+\left(\frac{3}{2}\right)^2 \)
\( \displaystyle AD^2 = \frac{45}{4} \)
$AD>0$より、\( \displaystyle AD = \frac{3\sqrt{5}}{2} \)
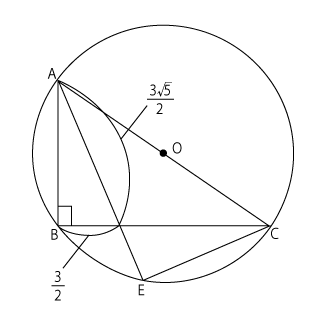
これにより、$△ABD$の3辺の長さがすべてわかったことになります。そして、点$E$を書き加えたものが右の図になりますが、問題文に$△AEC$に着目するようにあります。ということは、$△ABD$と$△AEC$は相似の関係になっていないかと考えることができそうです。その方針で考えてみましょう。
$△ABC$は$∠ABC = 90°$の直角三角形であり、右の図のように$∠ABC$は外接円$O$における円周角になっています。円周角が90°なのですから、辺$AC$は円$O$の直径になっています。よって、同じ$AC$の円周角になっている$∠AEC$も90°です。よって、$∠ABD = ∠AEC$です。
そして、$AE$は$∠BAC$の二等分線になっているので、$∠BAD = ∠EAC$
2組の角がそれぞれ等しいので、$△ABD$∽$△AEC$
\( ∴AB:AE = AD:AC \)
\( \displaystyle 3:AE = \frac{3\sqrt{5}}{2}:5 \)
\( \displaystyle \frac{3\sqrt{5}}{2}AE = 15 \)
\( \displaystyle AE = 15×\frac{2}{3\sqrt{5}} = \frac{30\sqrt{5}}{3×5} = 2\sqrt{5} \)
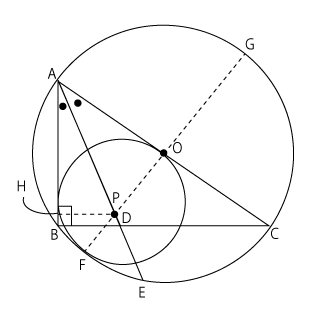
また、$P$や$F$,$G$の位置関係を示したものが右の図になりますが、$P$と辺$AB$との接点を$H$とすると、$PH$は円$P$の半径になっています。すると、$△APH$と$△ADB$において、
\( ∠AHP = ∠ABD = 90° \)
共通の角なので\( ∠HAP = ∠BAD \)
2組の角がそれぞれ等しいので、$△APH$∽$△ADB$
これより、\( AP:AD = PH:DB \)
$PH$は円$P$の半径ですから、\( \displaystyle AP:\frac{3\sqrt{5}}{2} = r:\frac{3}{2} \)
\( \displaystyle \frac{3}{2}AP = \frac{3\sqrt{5}}{2}r \)
\( 3AP = 3\sqrt{5}r \)
\( AP = \sqrt{5}r \)
そして、円$P$と円$O$の接点$F$と$P$を結んだ直線$FP$は図のとおり、両方の円の中心を通っています。つまり、$FG$の長さは円$O$の直径と等しいことになります。円$O$の直径は$AC$ですから、その長さは5です。
$FP$は円$P$の半径なので、\( PG = FG-FP = 5-r \)
次に、$r$の長さを求めますが、ここまで$AP$,$PG$を求めてきました。問題文に「方べきの定理により」とあるとおり、方べきの定理を使うと$r$を計算できるからです。方べきの定理とはこのような定理です。
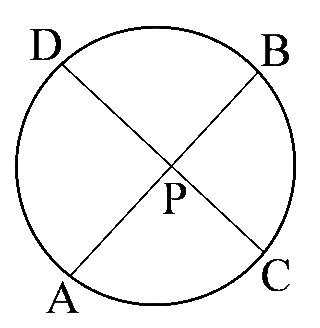
円周上に4点$A$,$B$,$C$,$D$があり、右の図のように円の内部や外部で$AB$と$CD$が交わっていれば、
\( PA×PB = PC×PD \)
(証明)
$△PAD$と$△PCB$において、
円周角の定理より、\( ∠PAD = ∠PCB \)
円周角の定理より、\( ∠PDA = ∠PBC \)
2組の角がそれぞれ等しいので、$△PAD$∽$△PCB$
よって、\( PA:PC = PD:PB \)なので\( PA・PB = PC・PD \)
$AP$と$PG$を求めましたが、この部分を含んでいる直線は$AE$と$FG$です。この方べきの定理を使って、円$O$に$AE$と$FG$の2本の直線が交差していると考えれば、
\( PA・PE = PF・PG \)
$PE$は$AE$から$AP$を引けば求まります。そして、$PF$は図からわかるとおり、円$P$の半径ですから、
\( \sqrt{5}r・(2\sqrt{5}-\sqrt{5}r) = r・(5-r) \)
\( r \neq 0 \)より、\( \sqrt{5}・(2\sqrt{5}-\sqrt{5}r) = 5-r \)
\( 10-5r = 5-r \)
\( 4r = 5 \)
\( \displaystyle r = \frac{5}{4} \)
さて、$△ABC$の内接円$Q$の半径を考えます。これを$q$とおきます。三角形の面積と内接円の半径について、(三角形の3辺の和)×(内接円の半径)に2分の1をかけたものが面積になりますから、$△ABC$の面積を考えます。$△ABC$は直角三角形ですから、その面積は
\( \displaystyle BC×AB×\frac{1}{2} = 4×3×\frac{1}{2} = 6 \)
よって、
\( \displaystyle \frac{1}{2}×(3+4+5)×q = 6 \)
\( 6q = 6 \)
\( q = 1 \)
次に、$AQ$の長さについてですが、内接円の中心は三角形のそれぞれの頂点の二等分線が交わったところにあります。つまり、$Q$は直線$AD$上にありますから、さっきの$AP$を求めたやり方と同じ方法で求めることができるはずです。
つまり、円$Q$と辺$AB$の接点を$I$とすると、$△AQI$と$△ADB$は相似ですから、
\( AQ:AD = QI:DB \)
$QI$はさっき求めた円$Q$の半径なので、\( \displaystyle AQ:\frac{3\sqrt{5}}{2} = 1:\frac{3}{2} \)
\( \displaystyle \frac{3}{2}AQ = \frac{3\sqrt{5}}{2} \)
\( \displaystyle AQ = \frac{3\sqrt{5}}{2}×\frac{2}{3} = \sqrt{5} \)
そして、$AH$の長さですが、これも$AQ$と同じように三角形の相似を利用して求めることができそうですね?なぜなら、だいぶ前に$△APH$∽$△ADB$を示しましたから、これを使えば、
\( AH:AB = PH:DB \)
$PH$、つまり円$P$の半径は\( \displaystyle \frac{5}{4} \)と求まっていましたから、\( \displaystyle AH:3 = \frac{5}{4}:\frac{3}{2} \)
\( \displaystyle \frac{3}{2}AH = \frac{15}{4} \)
\( \displaystyle AH = \frac{15}{4}×\frac{2}{3} = \frac{5}{2} \)
最後に、点$H$が同じ円の円周上にあるかということについて調べる問題があります。4つの点が同じ円の円周上にあるかを調べる方法は複数ありますが、そのうちの一つが方べきの定理の逆を使うというものです。方べきの定理の逆とはこのようなものです。

2本の直線$AB$と$CD$が点$P$で交わっていて、\( PA・PB = PC・PD \)が成り立っていれば、4つの点$A$,$B$,$C$,$D$は1つの円周上にある。
(証明)
$△PAC$と$△PDB$において、
\( PA・PB = PC・PD \)が成り立っているので、\( PA:PC = PD:PB \)
対頂角は等しいので、\( ∠APC = ∠DPB \)
2組の辺の比とその間の角がそれぞれ等しいので、$△PAC$∽$△PDB$
よって、\( ∠PAC = ∠PDB \)
円周角の定理の逆より、4つの点$A$,$B$,$C$,$D$は1つの円周上にある。
さきほどまで、$AH$や$AQ$を求めてきました。よって、$AH$,$AQ$,$AB$などの長さをあてはめてこの方べきの定理の逆が成り立つかどうかを調べてみましょう。
(a)についてですが、$AH$,$AB$,$AD$,$AQ$をあてはめると、
\( \displaystyle AH・AB = \frac{5}{2}・3 = \frac{15}{2} \)
\( \displaystyle AQ・AD = \sqrt{5}・\frac{3\sqrt{5}}{2} = \frac{15}{2} \)
\( AH・AB = AQ・AD \)が成り立ちますので、$H$,$B$,$D$,$Q$は1つの円周上にある、つまり、点$H$は3点$B$,$D$,$Q$を通る円の周上にあります。なので、(a)は正です。
(b)についてですが、$AH$,$AB$,$AE$,$AQ$をあてはめると、
\( AH・AB \)はさっき求めたとおり、\( \displaystyle \frac{15}{2} \)
\( AQ・AE = \sqrt{5}・2\sqrt{5} = 10 \)
\( AH・AB \neq AQ・AE \)なので、$H$,$B$,$E$,$Q$は1つの円周上にはありません。つまり、点$H$は3点$B$,$E$,$Q$を通る円の周上にはありません。なので、(b)は誤りです。
答え.
ア 3 イ 2
ウ 3 エ 5 オ 2
カ 2 キ 5
ク 5 ケ 5 コ 5 サ 4
シ 1 ス 5 セ 5 ソ 2
タ ①