この問題のポイント
絶対値は絶対値記号の中身が0以上かちがうかで分けて考える!
関数の最大値や最小値、y = f(x)とy = g(x)のグラフの共有点はグラフを描いて考えるとわかりやすい!
\( |x+4| \)と\( |x+1| \)の2つがあるので、これらの絶対値記号をはずす必要があります。ただし、\( |A| \)は$A≧0$ならば$A$ですが$A<0$ならば$-A$として記号をはずす必要があります。(つまり、正の数ならばそのままでいいけれど、負の数ならば-(-3) = 3のようにして正の数にする必要があるということ)
この問題でも\( |x+4| \)と\( |x+1| \)は絶対値記号の中身が正の数になるのか負の数になるのかは決まっているわけではないので、正の数の場合、負の数の場合と分けて考える必要があります。それぞれについて分けて考えるとこのようになります。
\( |x+4| \)…
\( x+4≧0 \)、つまり\( x≧-4 \)のときは$x+4$
\( x+4<0 \)、つまり\( x<-4 \)のときは\( -(x+4) = -x-4 \)
\( |x+1| \)…
\( x+1≧0 \)、つまり\( x≧-1 \)のときは$x+1$
\( x+1<0 \)、つまり\( x<-1 \)のときは\( -(x+1) = -x-1 \)
よって、まとめるとこのようになります。
- \( x<-4 \)のとき…
\( y = |x+4|-|x+1| \)
\( = -x-4-(-x-1) \)
\( = -x-4+x+1 = -3 \) - \( -4≦x<-1 \)のとき…
\( y = |x+4|-|x+1| \)
\( = x+4-(-x-1) \)
\( = x+4+x+1 \)
\( = 2x+5 \) - \( -1≦x \)のとき…
\( y = |x+4|-|x+1| \)
\( = x+4-(x+1) \)
\( = x+4-x-1 = 3 \)
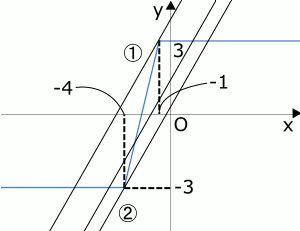
よって、\( y = |x+4|-|x+1| \)をグラフにすると右の図の青色で書いたものになるので、最大値は3で最小値は-3とわかります。
そして、このグラフと直線\( y = x+k \)の共有点について考えますが、\( y = x+k \)のグラフは$y$切片が$k$で傾きが1の直線です。ということで、そのグラフは図の黒色の直線のようになります。
この直線と青色のグラフが3個の共有点をもつには、\( y = x+k \)のグラフは図の①と②の間にある状態になる必要があります。その2本の直線の間における$y$切片の$k$の範囲を考えればいいということになります。
$y$切片の$k$の値が最大になるのは図の①のとき、つまり(-1,3)を通るときで、このときの$k$の値は
\( 3 = -1+k \)より\( k = 4 \)
$y$切片の$k$の値が最小になるのは図の②のとき、つまり(-4,-3)を通るときで、このときの$k$の値は
\( -3 = -4+k \)より\( k = 1 \)
ただし、①も②も、\( y = |x+4|-|x+1| \)のグラフとの共有点は2個しかありませんから、\( y = x+k \)のグラフは①や②の状態になってはダメで、必ず間にある状態になっていなければなりません。つまり、$y$切片が1や4となってはダメということなので、$k$の範囲は\( 1<k<4 \)です。
最後に、$x$軸方向に5,$y$軸方向に1だけ平行移動したグラフの方程式を求めます。\( y = f(x) \)のグラフを$x$軸方向に$p$,$y$軸方向に$q$だけ平行移動したグラフの方程式は、移動前の方程式の$x$に$x-p$,$y$に$y-q$を代入して計算すれば求まります。この問題でもそれをやってみましょう。
\( y = |x+4|-|x+1| \)の$x$に$x-5$,$y$に$y-1$を代入すると、
\begin{eqnarray} &&y-1 = |x-5+4|-|x-5+1|\\ &&y-1 = |x-1|-|x-4|\\ &&y = |x-1|-|x-4|+1 \end{eqnarray}
答え.
ア 3 イ -3 ウ 1 エ 4
オ -1 カ -4 キ 1