この問題のポイント
sin、cos、tanのどれか1つがわかっていればほかの2つも求めることができる!
三角比の角は45°までの角度であらわすことができる!
(1)sin、cos、tanのどれか1つの値がわかっていれば、ほかの2つの値を下にある公式を使って計算することができます。
1.\( \displaystyle \tanθ = \frac{\sinθ}{\cosθ} \)
2.\( \cos^2θ+\sin^2θ = 1 \)
3.\( \displaystyle 1+\tan^2θ = \frac{1}{\cos^2θ} \)
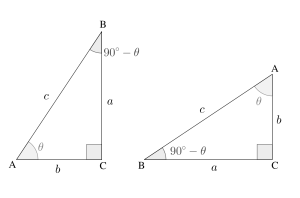
※証明
1.について、図の左側にある直角三角形において、
\( \displaystyle \tanθ = \frac{a}{b} \)
そして、\( \displaystyle \frac{\sinθ}{\cosθ} = \sinθ÷\cosθ \)なので、
\( \displaystyle \frac{a}{c}÷\frac{b}{c} = \frac{a}{c}×\frac{c}{b} = \frac{a}{b} \)
同じ値となるので、\( \displaystyle \tanθ = \frac{\sinθ}{\cosθ} \)
2.について、\( \displaystyle \sinθ = \frac{a}{c} \),\( \displaystyle \cosθ = \frac{b}{c} \)なので、
\( \cos^2θ+\sin^2θ \)
\( \displaystyle = \left(\frac{b}{c}\right)^2+\left(\frac{a}{c}\right)^2 \)
\( \displaystyle = \frac{b^2}{c^2}+\frac{a^2}{c^2} \)
\( \displaystyle = \frac{b^2+a^2}{c^2} \)
図の左側にある直角三角形において、三平方の定理より、
\( b^2+a^2 = c^2 \)なので、
\( \displaystyle \frac{b^2+a^2}{c^2} = \frac{c^2}{c^2} = 1 \)
よって、\( \cos^2θ+\sin^2θ = 1 \)が成り立ち、この両辺を\( \cos^2θ \)で割ると、
\( \displaystyle 1+\frac{\sin^2θ}{\cos^2θ} = \frac{1}{\cos^2θ} \)
\( \displaystyle 1+\left(\frac{\sinθ}{\cosθ}\right)^2 = \frac{1}{\cos^2θ} \)
\( \displaystyle 1+\tan^2θ = \frac{1}{\cos^2θ} \)と3.の式ができる
さて、問題を見てみると、\( \sinθ \)の値がわかっているので、2.の式を利用すると\( \cosθ \)の値は、
\( \displaystyle \cos^2θ+\left(\frac{1}{3}\right)^2 = 1 \)
\( \displaystyle \cos^2θ+\frac{1}{9} = 1 \)
\( \displaystyle \cos^2θ = \frac{8}{9} \)
$θ$は鋭角なので、\( \cosθ>0 \)のため、\( \displaystyle \cosθ = \frac{2\sqrt{2}}{3} \)
1.の式を利用して、\( \tanθ \)は、
\( \displaystyle \frac{\sinθ}{\cosθ} \)
\( \displaystyle = \frac{1}{3}÷\frac{2\sqrt{2}}{3} \)
\( \displaystyle = \frac{1}{3}×\frac{3}{2\sqrt{2}} = \frac{1}{2\sqrt{2}} = \frac{\sqrt{2}}{4} \)
(2)さっきの(1)の解説にて赤枠で囲んだ部分にある式を利用します。3.の式を利用すると、
\( \displaystyle 1+\tan^2x = \frac{1}{\cos^2x} \)
\( \displaystyle \frac{1}{\cos^2x} = 1+\tan^2x \)
\( \displaystyle \cos^2x = \frac{1}{1+\tan^2x} \)
\( 0°<x<90° \)より、\( \cos{x}>0 \)なので、\( \displaystyle \cos{x} = \frac{1}{\sqrt{1+\tan^2x}} \)
そして、1.の式を変形すると、\( \tanθ・\cosθ = \sinθ \)より、
\( \displaystyle \sin{x} = \tan{x}・\frac{1}{\sqrt{1+\tan^2x}} \)
\( \displaystyle = \frac{\tan{x}}{\sqrt{1+\tan^2x}} \)
(3)まず\( \sin{(90°-θ)} \)のほうですが、これについては下の式のように変換することができます。
\( \sin{(90°-θ)} = \cosθ \)
\( \cos{(90°-θ)} = \sinθ \)
\( \displaystyle \tan{(90°-θ)} = \frac{1}{\tanθ} \)
※証明
(1)の解説にあった2つの三角形を使って証明できる。左側にある三角形を、$90°-θ$の角のほうが下になるように倒したのが右側の三角形である。
図の右側の三角形より、\( \displaystyle \sin{(90°-θ)} = \frac{b}{c} \)
これは左側の三角形における\( \cosθ \)に等しい。
図の右側の三角形より、\( \displaystyle \cos{(90°-θ)} = \frac{a}{c} \)
これは左側の三角形における\( \sinθ \)に等しい。
図の右側の三角形より、\( \displaystyle \tan{(90°-θ)} = \frac{b}{a} \)
これは左側の三角形の\( \tanθ \)の逆数である。
よって、\( \sin{(90°-θ)} \)を求めるには\( \cosθ \)を求めたらよいということになります。問題では、\( \sinθ \)の値が与えられていましたから、\( \cos^2θ+\sin^2θ = 1 \)より、
\( \displaystyle \cos^2θ+\left(\frac{12}{13}\right)^2 = 1 \)
\( \displaystyle \cos^2θ+\frac{144}{169} = 1 \)
\( \displaystyle \cos^2θ = \frac{25}{169} \)
\( 0°≦θ≦90° \)より、\( \displaystyle \cosθ>0 \)なので、\( \displaystyle \cosθ = \frac{5}{13} \)と求まるので、\( \displaystyle \sin{(90°-θ)} = \frac{5}{13} \)
次に\( \tan{(180°-θ)} \)のほうですが、これについては下の式のように変換することができます。
\( \sin{(180°-θ)} = \sinθ \)
\( \cos{(180°-θ)} = -\cosθ \)
\( \tan{(180°-θ)} = -\tanθ \)
※証明
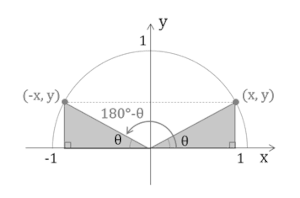
上の図のように半径1の円のところに$θ$と$180°-θ$の角をとると、座標は上の図に示したとおりになる。
すると、\( \displaystyle \sinθ = \frac{y}{1} = y \),\( \displaystyle \sin{(180°-θ)} = \frac{y}{1} = y \)
よって、\( \sin{(180°-θ)} = \sinθ \)
\( \displaystyle \cosθ = \frac{x}{1} = x \),\( \displaystyle \cos{(180°-θ)} = \frac{-x}{1} = -x \)
よって、\( \cos{(180°-θ)} = -\cosθ \)
\( \displaystyle \tanθ = \frac{y}{x} \),\( \displaystyle \tan{(180°-θ)} = \frac{y}{-x} = -\frac{y}{x} \)
よって、\( \tan{(180°-θ)} = -\tanθ \)
よって、\( \tan{(180°-θ)} \)を求めるには\( \tanθ \)を求めたらよいということになります。\( \sinθ \)の値は与えられていますし、\( \cosθ \)もさっき求めましたから、
\( \displaystyle \tanθ = \frac{\sinθ}{\cosθ} \)
\( \displaystyle = \frac{12}{13}÷\frac{5}{13} \)
\( \displaystyle = \frac{12}{13}×\frac{13}{5} = \frac{12}{5} \)
\( \displaystyle ∴\tan{(180°-θ)} = -\frac{12}{5} \)
答え.
(1)
\( \displaystyle \cosθ = \frac{2\sqrt{2}}{3} \),\( \displaystyle \tanθ = \frac{\sqrt{2}}{4} \)
(2)
\( \displaystyle \cos{x} = \frac{1}{\sqrt{1+\tan^2x}} \),\( \displaystyle \sin{x} = \frac{\tan{x}}{\sqrt{1+\tan^2x}} \)
(3)
ア 5 イ 13
ウ -12 エ 5