問題ページにもどる

この問題のポイント

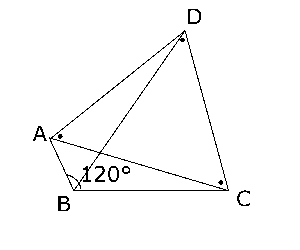
（１）〈指針〉

四角形$ABCD$を図にすると右のようになります。\( CD = DA = AC \)なので、$△ACD$は正三角形ということがわかります。よって、$∠DAC$，$∠DCA$，$∠ADC$も60°ということがわかりますが、この程度のことまでしかわかりません。

この問題で証明しなければならない結論をよく見ると、辺の長さを比べるものとなっています。辺の長短についての定理として、次のようなものがあります。これが使えないかを考えてみましょう。

$AB$に向かい合う角は$∠ADB$で、$BD$に向かい合う角は$∠BAD$です。どちらも$△ACD$の1つの角が関係しています。その角との関係を使いながら、$∠ADB$が$∠BAD$より小さいことを示すといいでしょう。

〈証明〉

\( CD = DA = AC \)より、$△ACD$は正三角形なので、\( ∠ADC = ∠DAC = 60° \)
ここで、
\( ∠ADB = ∠ADC-∠CDB = 60°-∠CDB \)
\( ∠BAD = ∠DAC+∠BAC = 60°+∠BAC \)
これより、\( ∠ADB＜∠BAD \)
$AB$に向かい合う角は$∠ADB$で、$BD$に向かい合う角は$∠BAD$なので、\( AB＜BD \)

解答のチェックポイント

• 角の大小はその向かい合う辺の長短と一致する性質を利用しているか
• $∠ADB$は60°より小さく、$∠BAD$は60°より大きいことを示しているか

（２）$△ACD$は正三角形なので、$∠ADC$ = 60°ですが、$∠ABC$ = 120°ですから、この2つの角をたすと180°です。ということは、この四角形$ABCD$は円に内接することがわかります。なぜなら、このような定理があるからです。

つまり、1.を根拠に四角形$ABCD$は円に内接するとわかるのですが、これに気づけるかどうかがポイントになります。

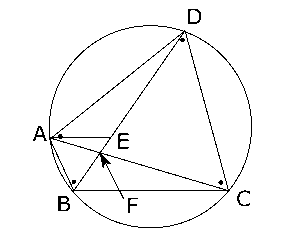
右の図のように円に内接することになりますが、円に内接しているということは、円周角の性質などを使って考えることができるということになります。つまり、どちらも弧$AD$の円周角ですから、●で示されているとおり、
\( ∠ACD = ∠ABD = 60° \)

そして、\( AB = BE \)なんですから、$△ABE$は二等辺三角形とわかりますから、
\( ∠BAE = ∠BEA \)

ここで、$∠ABE$ = 60°より、$∠BAE$と$∠BEA$はそれぞれ、
(180°-60°)÷2 = 60°
よって、$∠BAE$ = 60°とわかり、同時に$△ABE$は実は正三角形だということもわかりました。

（３）〈指針〉

\( AB = BE \)ということはわかっていますから、$BC$と$ED$が等しいということがわかれば証明ができそうです。

中学数学で、「この辺とこの辺が等しい」ということを証明する方法で一番多かったのが、三角形の合同を利用して証明するというものでしたね？（２）の解説の図を見ると、三角形が多くあるので、その方法が使えそうだと考えてみましょう。

すると、$△ABC$と$△AED$の合同を証明できれば\( BC = ED \)が証明できそうだと考えられます。それを使って\( AB+BC = BD \)を証明するとよいでしょう。

〈証明〉

$△ABC$と$△AED$において、
仮定より、\( AC = AD \)…①
\( AB = BE \)で$∠BAE$ = 60°なので、$△ABE$は正三角形といえるので、\( AB = AE \)…②
ここで、$AC$と$BD$の交点を$F$とすると、
\( ∠BAC = ∠BAE-∠EAF = 60°-∠EAF \)…③
\( ∠EAD = ∠DAC-∠EAF = 60°-∠EAF \)…④
③，④より、\( ∠BAC = ∠EAD \)…⑤
①，②，⑤より、2辺とその間の角がそれぞれ等しいので、$△ABC$≡$△AED$
よって、\( BC = ED \)
よって、\( AB+BC = BE+ED = BD \)

答え．
（１）（上の〈証明〉参照）
（２）60°
（３）（上の〈証明〉参照）

©All Rights Reserved