この問題でおさえておきたいこと
入射角と反射角は等しいということを意識して光がどう通るかを描こう!
解答
(1)(例)
$∠a$は入射角、$∠b$は反射角なので、$∠a$と$∠b$の大きさは等しい。
(2)
70°
(3)
ア,イ,ウ,エ
(4)
ア
重要事項のまとめ
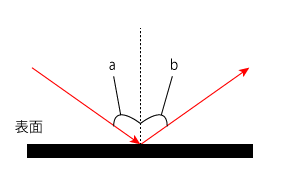
反射…光が鏡などの物体の表面にあたってはね返ること
入射角…鏡などの表面に立てた垂線と入射光のなす角(右の図のaの角)
反射角…鏡などの表面に立てた垂線と反射光のなす角(右の図のbの角)
光の反射の性質…
入射角と反射角の大きさは必ず等しい
解説
(1)解答のチェックポイント
- $∠a$は入射角であることが示されているか
- $∠b$は反射角であることが示されているか
- $∠a$と$∠b$の大きさは等しいことが示されているか
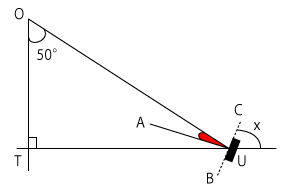
(2)$T$を通って$S$に届いているということは、光の道すじとして$OU$,$UT$を通っていることになりますが、その部分を拡大したのが右の図ですね。
光があたって反射しているということは、(1)でもふれていたとおり、入射角と反射角の関係が隠れているということであり、先の問題にふれていたということは、それを使って考えるということが多いです。そこで、鏡に垂線をひいて、右の図のように、$A$,$B$,$C$とおいてみます。
この三角形について、$∠OUT$ = 180°-90°-50° = 40°です。そして、入射角と反射角は等しいから、右の図の赤い印をつけている角度は$∠OUT$のちょうど半分となります。よって、$∠OUA$ = 40°÷2 = 20°です。
ここで、$AU$は鏡に対してひいた垂線なんですから、$∠AUC$ = 90°のはずです。$∠OUC$はその直角から$∠OUA$をひいた角なので、$∠OUC$ = 90°-20° = 70°です。
ということは、$x$の角度は、直線(180°)から$∠OUT$と$∠OUC$をひいた角なんですから、
$x$ = 180°-40°-70° = 70°
(3)入射角と反射角は等しいんですから、$∠OUT$と同じ角度で光が反射するはずです。ということは、$UT$を対称の軸にして$△OUT$と線対称の図形ができると考えられます。
ですから、作図するときは、$OT$と同じ長さをコンパスでとって、$OT$の延長線上に印をつけておきます。その印をつけたところと鏡2を直線で結ぶと下の図の赤線のとおりとなります。
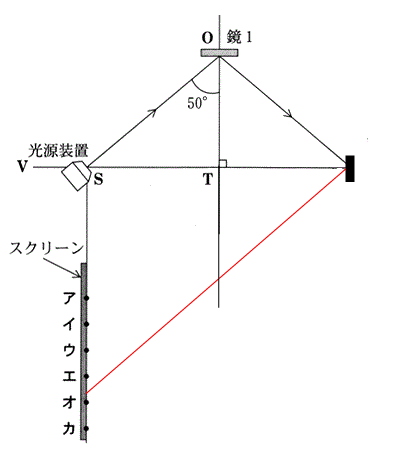
そして、鏡2が垂直になるまでには、光はスクリーンのア、イ、…と順番に通っていくと考えられますから、光はエまでは通過するけれども、オは通過していくことはないということになります。よって、通過する順に並べると、ア,イ,ウ,エとなります。
(4)鏡に像を映すと、左右が反対になって見えます。$V$の位置から見ているものは、鏡に2回映されたものですから、左右が反対になったものがまた反対にされているということで、左右が元に戻った状態ということになります。
図4の文字は$O$から見た状態なんですから、これが元の状態の文字です。よって、これと同じ状態で見えてるわけですから、アが正解となります。