問題ページにもどる

この問題でおさえておきたいこと

光の強さと光合成速度の関係をグラフを通しておさえる！
陽生植物と陰生植物の違いを理解しよう！

解答
問1
（１）A植物…500ルクス　　　B植物…1000ルクス
（２）A植物…1500ルクス　　　B植物…3500ルクス
（３）1500ルクス以下
（４）A植物…1000ルクス　　　B植物…2000ルクス
問2
①…陽生植物　　　②…陰生植物

重要事項のまとめ

・光合成曲線とは

植物にさまざまな光の強さをあてたときに、二酸化炭素の吸収速度や吸収量がどうなるかを示したグラフを光合成曲線という。

・光の強さと光合成速度

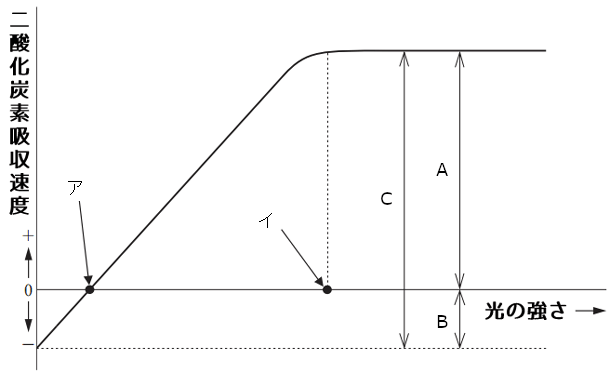
高校　生物　問題演習　光合成曲線のグラフ

光の強さが0のときは光合成はしないで、呼吸だけをしている。そのため、二酸化炭素吸収速度（吸収量）はマイナス、つまり吸収せずに放出する速度（放出量）が算出されている。

↓

光の強さを0から大きくしていくと、光合成が少しはされるようになる。しかし、そこまで光が強くないという状態であれば、まだ光合成より呼吸のほうががさかんなので、二酸化炭素吸収速度（吸収量）はマイナスの状態が続く。

↓

やがて、ある強さまで光を強くすると（図のアの点）、二酸化炭素の吸収速度（吸収量）と呼吸による放出速度（放出量）が同じになり、吸収速度（吸収量）が0になる。このときの光の強さ（図のアの点の強さ）を光補償点という。

↓

さらに光を強くしていくと、呼吸より光合成のほうがさかんとなり、二酸化炭素の吸収速度（吸収量）が上がっていく。

↓

やがて、光合成の活動が限界となり、これ以上光を強くしても二酸化炭素の吸収速度（吸収量）が上がらないようになる（図のイの点）。これ以上強くしても光合成速度が変わらなくなる光の強さ（図のイの点の強さ）を光飽和点という。

また、光合成曲線でこれらのことが読み取れる。

・陽生植物と陰生植物

明るい場所でしか生育できない植物を陽生植物、暗い場所でも生育することができる植物を陰生植物という。

一般的に陰生植物より陽生植物のほうが光合成速度や呼吸速度が大きい
また、陰生植物より陽生植物のほうが光補償点や光飽和点が高い（明るい場所でしか生育できないので、かなりの光を必要とするため）。

解説

問1

（１）「重要事項のまとめ」にもあるとおり、光補償点とは二酸化炭素の吸収量が0になる光の強さのことです。その光の強さをグラフから読み取りましょう。単位としてグラフの横軸にも示されている「ルクス」をつける必要もあります。

（２）「重要事項のまとめ」にもあるとおり、光飽和点とは光合成速度が変わらなくなる光の強さのことです。その光の強さをグラフから読み取ることとなります。この問題も、単位としてグラフの横軸にも示されている「ルクス」をつけます。

（３）光合成速度について同じになるときということであり、見かけの光合成速度についてではないことに注意です。つまり、「重要事項のまとめ」にあるとおり、見かけの光合成速度と呼吸速度を足したもので考える必要があるということになります。

グラフより、A植物の呼吸速度は3mg、B植物の呼吸速度は6mgとわかります。光の強さについてはこれから求めることになるためわかりませんから、見かけの光合成速度がいくらかについて判断はできません。なので、A植物とB植物の見かけの光合成速度をそれぞれ$a$mg，$b$mgとおきます。

すると、A植物の光合成速度は$(a+3)$mg，B植物の光合成速度は$(b+6)$mgとなります。これらが等しくなればいいので、
$a+3 = b+6$
$∴a = b+3$

この式より、A植物の見かけの光合成速度が、B植物のそれより3mg多くなっているときが条件に合致しているということになります。グラフより、そのような状態になっているのは1500ルクス以下のときです。

（４）A植物から考えてみましょう。さっきの（３）にて呼吸量は3mgと説明しましたが、問題文より、これは3時間という長さでの量です。呼吸は光がなくてもされますから、1日、つまり24時間の呼吸量は3×(24÷3) = 24mgです。

さっきの（３）と同じように、見かけの光合成量を$a$mgとすると、光合成速度は$(a+3)$mgです。12時間だけ光を照射するわけですから、光合成がされるのはそのときだけです。なので、1日における光合成量は$(a+3)×(12÷3) = 4(a+3)$mgです。

これが同じになるんですから、$4(a+3) = 24$
これを解くと、$a = 3$
つまり、A植物の見かけの光合成量が3mgのときの光の強さが答えなので、1000ルクスと求まります。

B植物についても同様に考えます。
1日の呼吸量は6×(24÷3) = 48mg
見かけの光合成量を$b$mgとすると、1日の光合成量は$(b+6)×(12÷3) = 4(b+6)$mg

$4(b+6) = 48$を解くと、$b = 6$
B植物の見かけの光合成量が6mgになっているときの光の強さは2000ルクスです。

問2

「重要事項のまとめ」を参照してください